如图，正方形 $ ABCD $ 和四边形 $ ACEF $ 所在的平面互相垂直．$ EF\parallel AC $，$ AB= \sqrt 2 $，$ CE=EF=1 $．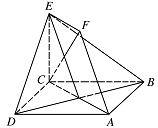
【难度】
【出处】
2010年高考北京卷（文）
【标注】
-
求证：$ AF\parallel 平面 BDE $；标注答案略解析设 $ AC $ 与 $ BD $ 交于点 $ G $．
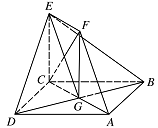因为 $EF\parallel AG$，且 $EF=1$，$AG={\dfrac{1}{2}}AC=1$，所以四边形 $AGEF$ 为平行四边形．
所以 $ AF\parallel EG $．
因为 $ EG\subset 平面 BDE $，$ AF\not\subset 平面 BDE $，
所以 $ AF\parallel 平面 BDE $． -
求证：$ CF\perp 平面 BDE $．标注答案略解析连接 $ FG $．
因为 $ EF\parallel CG $，$ EF=CG=1 $，且 $ CE=1 $，所以四边形 $ CEFG $ 为菱形．
所以 $ CF\perp EG $．
因为四边形 $ ABCD $ 为正方形，所以 $ BD\perp AC $．
又因为平面 $ ACEF\perp$ 平面 $ABCD $，且 $ 平面 ACEF\cap 平面 ABCD=AC $，
所以 $ BD\perp 平面 ACEF $．所以 $ CF\perp BD $．
又 $ BD\cap EG=G $，所以 $ CF\perp 平面 BDE $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
