如图，正方形 $ ABCD $ 和四边形 $ ACEF $ 所在的平面互相垂直，$ CE\perp AC $，$ EF\parallel AC $，$ AB= \sqrt 2 $，$ CE=EF=1 $．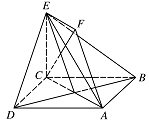
【难度】
【出处】
2010年高考北京卷（理）
【标注】
-
求证：$ AF\parallel 平面 BDE $；标注答案略解析设 $ AC $ 与 $ BD $ 交与点 $ G $．
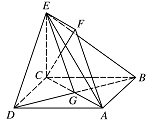因为 $ EF\parallel AG $，且 $ EF=1 $，$AG=\dfrac{1}{2}AC=1$．
所以四边形 $ AGEF $ 为平行四边形．
所以 $ AF\parallel 平面 EG $，
因为 $EG \subset 平面 BDE$，$AF \not\subset 平面 BDE$，
所以 $ AF\parallel 平面 BDE $． -
求证：$ CF\perp 平面 BDE $；标注答案略解析因为正方形 $ ABCD $ 和四边形 $ ACEF $ 所在的平面相互垂直，且 $ CE \perp AC $，
所以 $CE \perp 平面ABCD $．
如图，以 $ C $ 为原点，建立空间直角坐标系 $C- xyz$．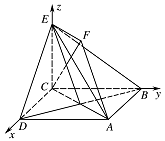
则\[C\left(0,0,0\right),A\left( \sqrt 2 , \sqrt 2 ,0\right),B\left(0, \sqrt 2 ,0\right).\]所以\[\overrightarrow {CF} = \left(\dfrac{{\sqrt 2 }}{2},\dfrac{{\sqrt 2 }}{2},1\right) , \overrightarrow {BE} = \left(0, - \sqrt 2 ,1\right) , \overrightarrow {DE} = \left( - \sqrt 2 ,0,1\right) .\]所以\[\overrightarrow {CF} \cdot \overrightarrow {BE} = 0 - 1 + 1 = 0 , \overrightarrow {CF} \cdot \overrightarrow {DE} = - 1 + 0 + 1 = 0.\]所以 $CF \perp BE$，$CF \perp DE$．所以 $CF \perp 平面 BDE $． -
求二面角 $ A-BE-D $ 的大小．标注答案略解析由（2）知，$\overrightarrow {CF} = \left(\dfrac{{\sqrt 2 }}{2},\dfrac{{\sqrt 2 }}{2},1\right)$ 是平面 $ BDE $ 的一个法向量．
设平面 $ ABE $ 的法向量 $\overrightarrow n = \left(x,y,z\right)$，则\[\overrightarrow n \cdot \overrightarrow {BA} = 0 , \overrightarrow n \cdot \overrightarrow {BE} = 0 .\]即\[\begin{cases} \left(x,y,z \right) \cdot \left(0, - \sqrt 2 ,1\right) = 0, \\ \left(x,y,z\right) \cdot \left(\sqrt 2 ,0,0\right) = 0, \end{cases} \]所以 $x = 0$，且 $z = \sqrt 2 y$，令 $y = 1$，则 $z = \sqrt 2 $．所以 $\overrightarrow n = \left(0,1,\sqrt 2 \right)$．
从而\[\cos \left\langle \overrightarrow n,\overrightarrow {CF} \right\rangle = \dfrac{{\overrightarrow n \cdot \overrightarrow {CF} }}{{ \left|\overrightarrow n \right| \left|\overrightarrow {CF} \right|}} = \dfrac{{\sqrt 3 }}{2} .\]因为二面角 $A - BE - D$ 为锐角，所以二面角 $A - BE - D$ 的大小为 $\dfrac{{\mathrm{\pi}} }{6}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
