题目 已知 $g(x)=x^2-2ax+1$ 在区间 $[1,3]$ 上的值域为 $[0,4]$． 问题1 求 $a$ 的值； 答案1 $1$ 解析1 根据题意，函数 $g(x)$ 的最大值必然在区间端点处取得，因此有\[g(1)=4\lor g(3)=4,\]解得 $a=-1$ 或 $a=1$．经检验可得 $a$ 的值为 $1$． 备注1 问题2 若不等式 $g\left(2^x\right)-k\cdot 4^x\geqslant 0$ 在 $x\in [1,+\infty)$ 上恒成立，求实数 $k$ 的取值范围； 答案2 $\left(-\infty,\dfrac 14\right]$ 解析2 设 $2^x=t$，则不等式即\[t^2-2t+1-k\cdot t^2\geqslant 0,\]即\[(1-k)t^2-2t+1\geqslant 0.\]题意即\[\forall t\geqslant 2,(1-k)t^2-2t+1\geqslant 0,\]也即\[\forall t\geqslant 2,1-k\geqslant -\left(\dfrac 1t\right)^2+\dfrac 2t,\]也即\[1-k\geqslant \dfrac 34,\]因此 $k$ 的取值范围是 $\left(-\infty,\dfrac 14\right]$． 备注2 问题3 若函数 $y=\dfrac{g\left(|2^x-1|\right)}{|2^x-1|}+k\cdot \dfrac{2}{|2^x-1|}-3k$ 有 $3$ 个零点，求实数 $k$ 的取值范围． 答案3 $(0,+\infty)$ 解析3 令 $t=|2^x-1|$ 且 $t\ne 0$，如图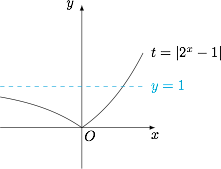．<img src="/static/images/977adda4b8c4631b9dc726d204c54c06.png" class="img-responsive" />$t$ 的不同取值与 $x$ 的取值个数 $n$ 的对应关系如下\[\begin{array} {c|ccc}\hline<br/>t&(-\infty,0)&(0,1)&[1,+\infty)\\ \hline<br/>n&0&2&1\\ \hline<br/>\end{array}\]考虑方程\[t^2-2t+1+2k-3kt=0,\]也即\[k=\dfrac{t^2-2t+1}{3t-2},\]记右侧函数为 $\varphi(t)$，则\[\varphi(t)=\dfrac 19\left[\left(3t-2\right)+\dfrac 1{3t-2}\right]-\dfrac 29,\]直线 $y=k$ 与 $\varphi(t)$ 图象有两个公共点，且横坐标分别在 $(0,1)$ 和 $[1,+\infty)$ 内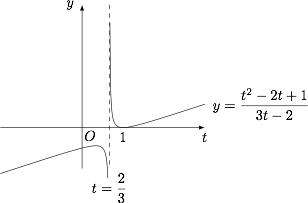．<img src="/static/images/4aae61b339b16dd5624fda7231856cc3.png" class="img-responsive" />如图，可得 $k$ 的取值范围是 $(0,+\infty)$． 备注3