如图，多面体 $A-PCBE$ 中，四边形 $PCBE$ 是直角梯形，且 $PC \perp BC$，$PE \parallel BC$，平面 $PCBE \perp$ 平面 $ABC$，$AC \perp BE$，$M$ 是 $AE$ 的中点，$N$ 是 $PA$ 上的点．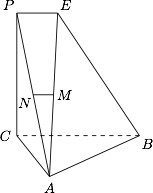
【难度】
【出处】
2017年清华大学THUSSAT测试理科数学（一测）
【标注】
-
若 $MN \parallel$ 平面 $ABC$，求证：$N$ 是 $PA$ 中点；标注答案略解析记 $PAE\cap ABC=l$，因为 $MN\parallel ABC$，根据线面平行的性质定理，有 $MN\parallel l$．
又 $PE\parallel BC$，所以 $PE\parallel ABC$，从而 $PE\parallel l$，于是 $PE\parallel MN$．
又 $M$ 是 $AE$ 的中点，于是 $N$ 是 $PA$ 的中点． -
若 $PE=\dfrac 13 BC$ 且 $AC=BC=PC$，求二面角 $E-AB-C$ 的余弦值．标注答案$\dfrac{\sqrt{22}}{11}$解析设 $PE=1$，$AC=BC=PC=3$，在平面 $PCBE$ 中作 $EH\perp BC$ 于 $H$，连接 $EH,AH$，如图．
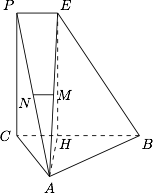根据题意，$PC\perp ABC$，于是 $PC\perp CA$，由 $AC\perp BE$，于是 $AC\perp PCBE$，因此 $\triangle ACB$ 是直角三角形，且 $C$ 为直角顶点．因此\[S_{\triangle ABH}=\dfrac 23S_{\triangle ABC}=\dfrac 23\cdot \dfrac 92=3,\]又\[\left.\begin{split}BE&=\sqrt{BH^2+EH^2}=\sqrt{13},\\
AE&=\sqrt{AH^2+EH^2}=\sqrt{19},\\
AB&=\sqrt{AC^2+BC^2}=\sqrt{18},\end{split}\right\}\Rightarrow S_{\triangle ABE}=3\cdot \sqrt{\dfrac{11}2},\]于是所求二面角的余弦值为\[\dfrac{3}{3\cdot \sqrt{\dfrac{11}2}}=\dfrac{\sqrt{22}}{11}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
