已知椭圆 $C:\dfrac{x^2}{a^2}+\dfrac{y^2}{12}=1$ 过点 $\left(2\sqrt3,-\sqrt3\right)$，点 $A,B$ 是椭圆上异于长轴端点的两个点．
【难度】
【出处】
无
【标注】
-
求椭圆 $C$ 的离心率；标注答案$\dfrac12$解析由题可以解得 $a=4$，结合 $c^2=a^2-b^2$，则椭圆的离心率为 $\dfrac12$．
-
已知直线 $l:x=8$，且 $AA_1\perp l$，垂足为 $A_1$，$BB_1\perp l$，垂足为 $B_1$，若 $D(3,0)$ 且 $S_{\triangle ABD}=\dfrac15S_{\triangle A_1B_1D}$，求 $AB$ 中点的轨迹方程．标注答案$(x-1)^2+\dfrac43y^2=1$解析设直线 $AB$ 与 $x$ 轴的交点为 $E$，直线 $A_1B_1$ 与 $x$ 的交点为 $F$，如图．
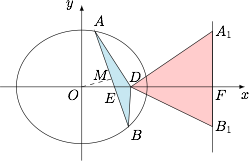则有$$\dfrac{S_{\triangle ABD}}{S_{\triangle A_1B_1D}}=\dfrac{DE}{DF}=\dfrac{DE}{5}=\dfrac15,$$再结合 $D(3,0)$，且直线 $AB$ 必不过 $(4,0)$，因此$$E(2,0),$$设直线 $AB$ 的中点坐标为 $(x,y)$，当 $x\ne2$ 时，根据垂径定理有$$\dfrac{y}{x-2}\cdot\dfrac{y}{x}=-\dfrac34,$$整理得$$(x-1)^2+\dfrac43y^2=1,$$经检验 $(2,0)$ 也符合上式，因此 $AB$ 的中点的轨迹方程是 $(x-1)^2+\dfrac43y^2=1$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
