如图所示,在长方体 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 中,$ AB=AD=1 $,$ AA_{1}=2 $,$ M $ 是棱 $ CC_{1} $ 的中点.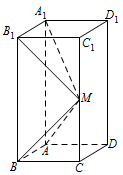

【难度】
【出处】
2010年高考湖南卷(文)
【标注】
-
求异面直线 $ A_{1}M $ 和 $ C_{1}D_{1} $ 所成的角的正切值;标注答案$\sqrt 2 $解析因为 $ C_{1}D_{1}\parallel B_{1}A_{1} $,所以 $\angle {M}{{A}_{1}}{{B}_{1}}$ 为异面直线 $ A_{1}M $ 与 $ C_{1}D_{1} $ 所成的角.
因为 $ A_{1}B_{1}\perp $ 平面 $ BCC_{1}B_{1} $,所以 $\angle A_{1}B_{1}M=90^\circ$.而\[A_{1}B_{1} =1,B_{1}M = \sqrt {{B_1}{C_1}^2 + {M{C_1}}^2} = \sqrt 2 ,\]故\[\tan \angle {M{A_1}{B_1}} = \dfrac{{{B_1}M}}{{{A_1}{B_1}}} = \sqrt 2 ,\]即异面直线 $ A_{1}M $ 和 $ C_{1}D_{1} $ 所成的角的正切值为 $\sqrt 2 $. -
证明:平面 $ ABM\perp $ 平面 $ A_{1}B_{1}M$.标注答案略解析由 $ A_{1}B_{1}\perp $ 平面 $ BCC_{1}B_{1} $,$BM \subset $ 平面 $ BCC_{1}B_{1} $,得\[ A_{1}B_{1}\perp BM. \quad \cdots \cdots ① \]由(1)知,\[{B_1}M = \sqrt 2 ,\]又\[BM = \sqrt {{BC}^2 + {CM}^2} = \sqrt 2 , {B_1}B = 2,\]所以\[{{B_1} M}^2 + {BM}^2 = {{B_1}B}^2,\]从而\[BM \perp {B_1}M, \quad \cdots \cdots ② \]又 $A_{1}B_{1} \cap B_{1}M=B_{1}$,再由 $ ① $,$ ② $ 得 $ BM\perp $ 平面 $ A_{1}B_{1}M $.
而 $BM \subset $ 平面 $ ABM $,因此平面 $ ABM\perp $ 平面 $ A_{1}B_{1}M $.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2