如图,是某城市通过抽样得到的居民某年的月均用水量(单位:吨)的频率分布直方图.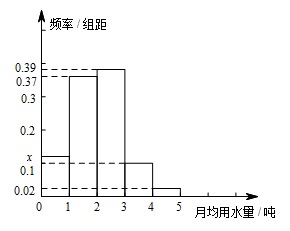

【难度】
【出处】
2010年高考湖南卷(理)
【标注】
-
求直方图中 $ x $ 的值;标注答案略解析依题意及频率分布直方图知 $0.02 + 0.1 + x + 0.37 + 0.39 = 1$,解得 $x = 0.12$.
-
若将频率视为概率,从这个城市随机抽取 $ 3 $ 位居民(看作有放回的抽样),求月均用水量在 $ 3 $ 至 $ 4 $ 吨的居民数 $ X $ 的分布列和数学期望.标注答案略解析由题意知,$X \sim B\left(3,0.1\right)$.因此
$P\left(X = 0\right) = {\mathrm{C}}_3^0 \times {0.9^3} = 0.729$,
$P\left(X = 1\right) = {\mathrm{C}}_3^1 \times 0.1 \times {0.9^2} = 0.243$,
$P\left(X = 2\right) = {\mathrm{C}}_3^2 \times {0.1^2} \times 0.9 = 0.027$,
$P\left(X = 3\right) = {\mathrm{C}}_3^3 \times {0.1^3} = 0.001$,
故随机变量 $ X $ 的分布列为\[ \begin{array}{|c|c|c|c|c|} \hline
X & 0 & 1 & 2 & 3 \\ \hline
P & 0.729 & 0.243 & 0.027 & 0.001 \\ \hline
\end{array}\]$ X $ 的数学期望为 $EX = 3 \times 0.1 = 0.3$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2