查看数据源：599165b92bfec200011dea5a
如图所示，在正方体 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 中，$ E $ 是棱 $D{D_1}$ 的中点．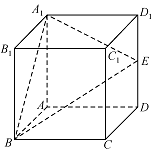 
【难度】
【出处】
2010年高考湖南卷（理）
【标注】
  1. 求直线 $ BE $ 和平面 $AB{B_1}{A_1}$ 所成的角的正弦值；
    标注
    答案
    略
    解析
    法一：
    设正方体的棱长为 $ 1 $．如图所示，以 $\overrightarrow {AB} ,\overrightarrow {AD} ,\overrightarrow {A{A_1}} $ 为单位正交基底建立空间直角坐标系 $O-xyz $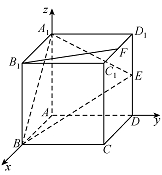． 依题意，得\[B\left(1,0,0\right),E\left(0,1,\dfrac{1}{2}\right),A\left(0,0,0\right),D\left(0,1,0\right).\]所以\[\overrightarrow {BE} = \left( - 1,1,\dfrac{1}{2}\right),\overrightarrow {AD} = \left(0,1,0\right).\]在正方体 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 中，因为 $AD \bot $ 平面 $AB{B_1}{A_1}$，
    所以 $\overrightarrow {AD} $ 是平面 $AB{B_1}{A_1}$ 的一个法向量．
    设直线 $ BE $ 和平面 $AB{B_1}{A_1}$ 所成的角为 $\theta $，则\[\sin \theta = \dfrac{{|\overrightarrow {BE} \cdot \overrightarrow {AD} |}}{{\left| {\overrightarrow {BE} } \right| \cdot \left| {\overrightarrow {AD} } \right|}} = \dfrac{1}{{\dfrac{3}{2} \times 1}} = \dfrac{2}{3} .\]即直线 $ BE $ 和平面 $AB{B_1}{A_1}$ 所成的角的正弦值为 $\dfrac{2}{3}$．
    法二：
    如图所示，取 $A{A_1}$ 的中点 $ M $，连结 $ EM,BM $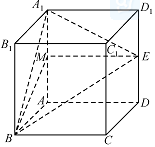． 因为 $ E $ 是 $D{D_1}$ 的中点，四边形 $AD{D_1}{A_1}$ 为正方形，所以 $EM\parallel AD$．
    又在正方体 $ABCD - {A_1}{B_1}{C_1}{D_1}$ 中，$AD \bot $ 平面 $AB{B_1}{A_1}$，所以 $EM \bot $ 平面 $AB{B_1}{A_1}$，
    从而 $ BM $ 为直线 $ BE $ 在平面 $AB{B_1}{A_1}$ 上的射影，$\angle EBM$ 为 $ BE $ 和平面 $AB{B_1}{A_1}$ 所成的角．
    设正方体的棱长为 $ 2 $，则 $EM = AD = 2$，$BE = \sqrt {{2^2} + {2^2} + {1^2}} = 3$．
    于是，在 ${\mathrm{Rt}}\triangle BEM$ 中，$\sin \angle EBM = \dfrac{{EM}}{{BE}} = \dfrac{2}{3} $，
    即直线 $ BE $ 和平面 $AB{B_1}{A_1}$ 所成的角的正弦值为 $\dfrac{2}{3}$．
  2. 在棱 ${C_1}{D_1}$ 上是否存在一点 $ F $，使 ${B_1}F\parallel $ 平面 ${A_1}BE$？证明你的结论．
    标注
    答案
    略
    解析
    法一：
    依题意，得\[{A_1}\left(0,0,1\right),\overrightarrow {B{A_1}} = \left( - 1,0,1\right),\overrightarrow {BE} = \left( - 1,1,\dfrac{1}{2}\right).\]设 $\overrightarrow n = \left( {x,y,z} \right)$ 是平面 ${A_1}BE$ 的一个法向量，则由\[\overrightarrow n \cdot \overrightarrow {B{A_1}} = 0,\overrightarrow n \cdot \overrightarrow {BE} = 0 ,\]得\[{\begin{cases}
    - x + z = 0, \\
    - x + y + \dfrac{1}{2}z = 0. \\
    \end{cases}}\]所以 $x = z$，$y = \dfrac{1}{2}z$．取 $z = 2$，得 $\overrightarrow n = \left( {2,1,2} \right)$．
    设 $ F $ 是棱 ${C_1}{D_1}$ 上的点，则 $F\left(t,1,1\right)\left(0 \leqslant t \leqslant 1\right).$
    又 ${B_1}\left(1,0,1\right),$ 所以 $\overrightarrow {{B_1}F} = \left(t - 1,1,0\right).$ 而 ${B_1}F \not\subset 平面 {A_1}BE$，于是\[ \begin{split}{B_1}F\parallel 平面 {A_1}BE &
    \Leftrightarrow \overrightarrow {{B_1}F} \cdot \overrightarrow n = 0 \\& \Leftrightarrow \left(t - 1,1,0\right) \cdot \left( {2,1,2} \right) = 0 \\& \Leftrightarrow 2\left(t - 1\right) + 1 = 0\\& \Leftrightarrow t = \dfrac{1}{2} \Leftrightarrow F 为 {C_1}{D_1} 的中点.\end{split}\]这说明在棱 ${C_1}{D_1}$ 上存在点 $ F $（$ {C_1}{D_1} $ 的中点），使 ${B_1}F\parallel 平面 {A_1}BE$．
    法二：
    在棱 ${C_1}{D_1}$ 上存在点 $ F $，使 ${B_1}F\parallel 平面 {A_1}BE$．
    事实上，如图所示，分别取 ${C_1}{D_1}$ 和 $CD$ 的中点 $F,G$，连结 $EG,BG,C{D_1},FG$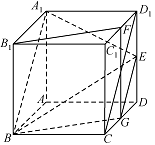． 因 ${A_1}{D_1}\parallel {B_1}{C_1}\parallel BC$，且 ${A_1}{D_1} = BC$，
    所以四边形 ${A_1}BC{D_1}$ 为平行四边形，因此 ${D_1}C\parallel {A_1}B$．
    又 $E,G$ 分别为 ${D_1}D$，$CD$ 的中点，所以 $EG\parallel {D_1}C$，从而 $EG\parallel {A_1}B $．
    这说明 ${A_1},B,G,E$ 共面．
    所以 $BG \subset $ 平面 ${A_1}BE$．
    因四边形 ${C_1}CD{D_1}$ 与 ${B_1}BC{C_1}$ 皆为正方形，$F,G$ 分别为 ${C_1}{D_1}$ 和 $CD$ 的中点，
    所以 $FG\parallel {C_1}C\parallel {B_1}B$，且 $FG = {C_1}C = {B_1}B$，
    因此四边形 ${B_1}BGF$ 为平行四边形，所以 ${B_1}F\parallel BG$．
    而 ${B_1}F \not\subset 平面 {A_1}BE$，$BG \subset 平面 {A_1}BE$，故 ${B_1}F\parallel 平面 {A_1}BE$．
题目 问题1 答案1 解析1 备注1 问题2 答案2 解析2 备注2
0.115607s