把一张纸卷到圆柱形的纸筒面上，卷上几圈．用剪刀斜着（即不与纸筒的轴平行或垂直）将纸筒剪断，再把卷着的纸展开．证明：纸的边缘形成的曲线是正弦型曲线．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
设纸筒的底面半径是 $1$，截面（椭圆面）与底面所成的二面角为 $\theta$，则 $\theta$ 为定值，截口的中心为 $O'$．
过 $O'$ 作圆柱的直截面，交截口曲线于两点．取其中一点为 $O$，在过点 $O$ 且与圆柱侧面相切的平面内，以点 $O$ 为坐标原点建立直角坐标系，使得 $Oy$ 轴是圆柱的一条母线．
设点 $P$ 是截口曲线上任意一点，点 $Q$ 是点 $P$ 在 $\odot O'$ 所在平面内的射影，过 $Q$ 作 $QH\perp O'O$，垂足为 $H$，连结 $PH$，则 $\angle PHQ$ 是截面与底面所成二面角的平面角，所以 $\angle PHQ=\theta$．
又设 $\angle QO'O=\alpha$，设展开后 $P$ 点坐标为 $(x,y)$，
分别计算 $x,y$ 与 $\alpha$ 的关系，得$$x=\overparen{OQ}=\alpha,y=QP=QH\cdot\tan\theta,$$而在 ${\rm Rt}\triangle QHO'$ 中，$QH=\sin\alpha$，所以 $y=\tan\theta\cdot\sin\alpha$．
这样我们就得到了展开后截口曲线上的点 $(x,y)$ 满足$$y=\tan\theta\cdot\sin x,$$即截口曲线展开后为正弦型曲线．如图：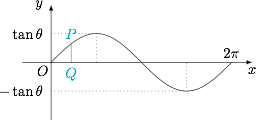
过 $O'$ 作圆柱的直截面，交截口曲线于两点．取其中一点为 $O$，在过点 $O$ 且与圆柱侧面相切的平面内，以点 $O$ 为坐标原点建立直角坐标系，使得 $Oy$ 轴是圆柱的一条母线．设点 $P$ 是截口曲线上任意一点，点 $Q$ 是点 $P$ 在 $\odot O'$ 所在平面内的射影，过 $Q$ 作 $QH\perp O'O$，垂足为 $H$，连结 $PH$，则 $\angle PHQ$ 是截面与底面所成二面角的平面角，所以 $\angle PHQ=\theta$．
又设 $\angle QO'O=\alpha$，设展开后 $P$ 点坐标为 $(x,y)$，
分别计算 $x,y$ 与 $\alpha$ 的关系，得$$x=\overparen{OQ}=\alpha,y=QP=QH\cdot\tan\theta,$$而在 ${\rm Rt}\triangle QHO'$ 中，$QH=\sin\alpha$，所以 $y=\tan\theta\cdot\sin\alpha$．
这样我们就得到了展开后截口曲线上的点 $(x,y)$ 满足$$y=\tan\theta\cdot\sin x,$$即截口曲线展开后为正弦型曲线．如图：
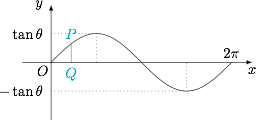
答案
解析
备注
