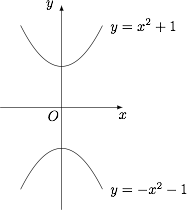
题目 依次回答下列问题： 问题1 在 $(x,y)$ 坐标平面上画出曲线 $C:y^2=x^4+2x^2+1$； 答案1 略 解析1 根据题意有$$y^2=(x^2+1)^2,$$所以曲线 $C$ 是由两条抛物线 $y=x^2+1$ 和 $y=-x^2-1$ 组成，它们的图象如图所示．<img src="/static/images/ae830007736f5fa68ba23f98e56aee35.png" class="img-responsive" /> 备注1 问题2 如果直线 $y=px+q$ 与曲线 $C$ 不相交，求参数 $p$ 和 $q$ 的取值范围． 答案2 $-1<q<1$ 且 $q\in \begin{cases} \left(2\sqrt{1-q},2\sqrt{1-q}\right),&0\leqslant q<1,\\<br/>\left(-2\sqrt{1+q},2\sqrt{1+q}\right),&-1<q<0.\end{cases}$ 解析2 直线 $y=px+q$ 与 $y$ 轴的交点的纵坐标就是 $q$，因为直线 $y=px+q$ 与曲线 $C$ 不相交，所以显然$$-1<q<1,$$<case>情形一</case> 当 $0\leqslant q<1$ 时，仅需考虑直线与抛物线 $y=x^2+1$ 不相交即可，即方程组$$\begin{cases} y=px+q,\\<br/>y=x^2+1,\end{cases}$$无解．联立消去 $y$ 后由判别式小于零可得$$p^2-4(1-q)<0,$$所以此种情形下 $p$ 的取值范围为 $(-2\sqrt{1-q},2\sqrt{1-q})$．<br/><case>情形二</case> 当 $-1<q<0$ 时，仅需考虑直线与抛物线 $y=-x^2-1$ 不相交即可，即方程组$$\begin{cases} y=px+q,\\<br/>y=-x^2-1,\end{cases}$$无解．联立消去 $y$ 后由判别式小于零可得$$p^2-4(1+q)<0,$$所以此种情形下 $p$ 的取值范围为 $(-2\sqrt{1+q},2\sqrt{1+q})$． 备注2