已知圆 $C:(x+4)^2+y^2=4$，点 $P(-3,0)$．圆心在 $y$ 轴上的动圆 $D$ 与圆 $C$ 外切，并且圆 $D$ 与 $y$ 轴相交于 $A,B$ 两点．
【难度】
【出处】
2007年第十八届"希望杯"全国数学邀请赛高二（二试）
【标注】
-
求 $\angle APB$ 的最大值；标注答案$\arctan\dfrac{12}{5}$解析如图．
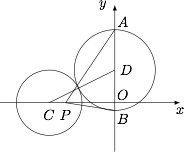设 $D(0,a)$，$A(0,a+r)$，$B(0,a-r)$，则根据到角公式，有\[\begin{split}\tan\angle APB&=\dfrac{\dfrac{a+r}{3}-\dfrac{a-r}{3}}{1+\dfrac{a+r}3\cdot \dfrac{a-r}3}\\
&=\dfrac{6r}{9+a^2-r^2}\\
&=\dfrac{6r}{9+(r+2)^2-4^2-r^2}\\
&=\dfrac{6r}{4r-3},\end{split}\]其中 $r\geqslant 2$．于是当 $r=2$ 时，$\angle APB$ 最大，为 $\arctan\dfrac{12}5$． -
当圆 $D$ 的圆心 $D$ 在 $y$ 轴移动时是否在 $x$ 轴上存在定点 $Q$ 使得 $\angle AQB$ 为定值，若存在，求出定点 $Q$ 的坐标；否则说明理由．标注答案存在点 $Q(\pm2\sqrt3,0)$解析设 $Q(b,0)$，则根据到角公式，有\[\begin{split}\tan\angle AQB&=\dfrac{\dfrac{a+r}{-b}-\dfrac{a-r}{-b}}{1+\dfrac{a+r}{-b}\cdot \dfrac{a-r}{-b}}\\
&=-\dfrac{2br}{a^2+b^2-r^2}\\
&=-\dfrac{2br}{(r+2)^2-16+b^2-r^2}\\
&=-\dfrac{2br}{4r+b^2-12},\end{split}\]于是 $\angle AQB$ 为定值等价于\[b^2-12=0,\]也即 $b=\pm 2\sqrt 3$，对应的 $\angle AQB=\arctan\left(-\dfrac b2\right)$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
