已知一个圆柱的轴截面为矩形 $ABCD$，如图，作一个过 $A,B$ 两点的截面将圆柱分成相同的两部分，记得到的截口曲线为 $\Gamma$．
【难度】
【出处】
无
【标注】
-
证明截口曲线的形状为椭圆；标注答案略解析记 $BD$ 的中点为 $O$，$AB$ 的中点为 $O_1$，连结 $OO_1$，并设 $AB=d,AD=h$，取截面上一点 $P$，作 $PR\perp BD$ 于 $R$，过 $R$ 作 $RT\perp AB$ 于 $T$，$PQ\perp$ 底面于点 $Q$，连结 $TQ$，如图，尝试探索 $PR$ 与 $OR$ 的关系：
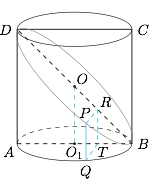由截面的对称性容易得到 $RT$ 与 $PQ$ 平行且相等，所以 $PR$ 与 $QT$ 平行且相等，从而有$$PR=QT=\sqrt{\dfrac{d^2}4-O_1T^2},$$所以 $O_1T^2+PR^2=\dfrac{d^2}4$．
又因为$$\dfrac{O_1T}{OR}=\dfrac{AB}{BD}=\dfrac d{\sqrt{d^2+h^2}},$$所以有$$\dfrac{d^2}{d^2+h^2}\cdot OR^2+PR^2=\dfrac {d^2}4,$$整理得$$\dfrac {4OR^2}{d^2+h^2}+\dfrac{4PR^2}{d^2}=1.$$这就证明了点 $P$ 在以 $O$ 为圆心，$BD$ 为长轴的椭圆上． -
将圆柱沿侧面展开，证明展开后的截口曲线是正弦型曲线一个周期的图象．标注答案略解析沿 $BC$ 将侧面剪开，设 $P$ 为截口曲线上一点，$PQ\perp AB$ 于 $Q$，设 $BQ=x,PQ=y$，如图，则 $BQ$ 对应圆柱中的弧 $AB$ 的长，尝试探索 $x,y$ 之间的函数关系：
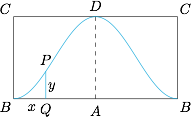在圆柱的底面圆上有$$\angle BO_1Q=\dfrac{\overparen{BQ}}{d/2}=\dfrac{2x}d,$$从而得到 $O_1T=\dfrac d2\cos\dfrac{2x}d$．
又$$y=PQ=RT=BT\cdot\tan\angle DBA=\left(\dfrac d2-\dfrac d2\cos\dfrac{2x}d\right)\cdot\dfrac hd,$$化简得到$$y=\dfrac h2\left(1-\cos\dfrac{2x}d\right).$$它的周期为 $\pi d$ 而截面展开图的矩形长为 $\pi d$，所以恰好为一个周期．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
