为了比较注射 A，B 两种药物后产生的皮肤疱疹的面积，选 $ 200 $ 只家兔做试验，将这 $ 200 $ 只家兔随机地分成两组，每组 $ 100 $ 只，其中一组注射药物 A，另一组注射药物 B．
附：${K^2} = \dfrac{{n{{\left(ad - bc\right)}^2}}}{{\left(a + b\right)\left(c + d\right)\left(a + c\right)\left(b + d\right)}}$\[\begin{array}{|c|c|c|c|c|c|} \hline
P\left(K^2 \geqslant k\right) & 0.100 & 0.050 & 0.025 & 0.010 & 0.001 \\ \hline
k & 2.706 & 3.841 & 5.024 & 6.635 & 10.828 \\ \hline
\end{array}\]
附：${K^2} = \dfrac{{n{{\left(ad - bc\right)}^2}}}{{\left(a + b\right)\left(c + d\right)\left(a + c\right)\left(b + d\right)}}$\[\begin{array}{|c|c|c|c|c|c|} \hline
P\left(K^2 \geqslant k\right) & 0.100 & 0.050 & 0.025 & 0.010 & 0.001 \\ \hline
k & 2.706 & 3.841 & 5.024 & 6.635 & 10.828 \\ \hline
\end{array}\]
【难度】
【出处】
2010年高考辽宁卷（理）
【标注】
-
甲、乙是 $ 200 $ 只家兔中的 $ 2 $ 只，求甲、乙分在不同组的概率；标注答案略解析甲、乙两只家兔分在不同组的概率为 $P = \dfrac{{2{\mathrm{C}}_{198}^{99}}}{{{\mathrm{C}}_{200}^{100}}} = \dfrac{{100}}{{199}}$．
-
下表 1 和表 2 分别是注射药物 A 和 B 后的试验结果．（疱疹面积单位：$ {\mathrm{mm}}^2 $）
表 1：注射药物 A 后皮肤疱疹面积的频数分布表\[\begin{array}{|c|c|c|c|c|} \hline
疱疹面积 & \left[60,65\right) & \left[65,70\right) & \left[70,75\right) & \left[75,80\right) \\ \hline
频数 & 30 & 40 & 20 & 10 \\ \hline
\end{array}\]表 2：注射药物 B 后皮肤疱疹面积的频数分布表\[\begin{array}{|c|c|c|c|c|c|} \hline
疱疹面积 & \left[60,65\right) & \left[65,70\right) & \left[70,75\right) & \left[75,80\right) & \left[80,85\right) \\ \hline
频数 & 10 & 25 & 20 & 30 & 15 \\ \hline
\end{array}\]（i）完成下面频率分布直方图，并比较注射两种药物后疱疹面积的中位数大小；
（ii）完成下面 $ 2\times 2 $ 列联表，并回答能否有 $ 99.9\% $ 的把握认为“注射药物 A 后的疱疹面积与注射药物 B 后的疱疹面积有差异”．
表 3：\[\begin{array}{|c|l|l|l|} \hline
& 疱疹面积小于 70 {\mathrm{mm}}^2 & 疱疹面积不小于 70 {\mathrm{mm}}^2 & 合计 \\ \hline
注射药物 {\text{A}} & a= & b= & \\ \hline
注射药物 {\text{B}} & c= & d= & \\ \hline
合计 & & & n= \\ \hline
\end{array}\]标注答案略解析（i）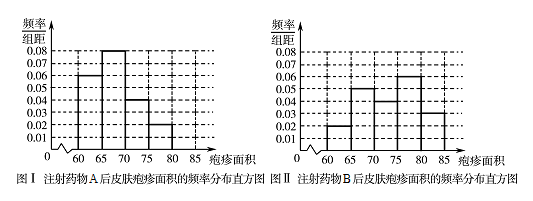
可以看出注射药物 A 后的疱疹面积的中位数在 $ 65 $ 至 $ 70 $ 之间，而注射药物 B 后的疱疹面积的中位数在 $ 70 $ 至 $ 75 $ 之间，所以注射药物 A 后疱疹面积的中位数小于注射药物 B 后疱疹面积的中位数．
（ii）表 3：\[\begin{array}{|c|l|l|l|} \hline
& 疱疹面积小于 70 {\mathrm{mm}}^2 & 疱疹面积不小于 70 {\mathrm{mm}}^2 & 合计 \\ \hline
注射药物 {\text{A}} & a=70 & b=30 &100 \\ \hline
注射药物 {\text{B}} & c=35 & d=65 &100 \\ \hline
合计 & 105& 95& n=200 \\ \hline
\end{array}\]所以\[ {K^2} = \dfrac{{200 \times {{\left(70 \times 65 - 35 \times 30\right)}^2}}}{{100 \times 100 \times 105 \times 95}} \approx 24.56 . \]由于 $ K^2>10.828 $，所以有 $ 99.9\% $ 的把握认为“注射药物 A 后的疱疹面积与注射药物 B 后的疱疹面积有差异”．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
