已知三棱锥 $ P-ABC $ 中，$ PA\perp 平面 ABC $，$ AB\perp AC $，$ PA=AC=\dfrac 1 2 AB $，$ N $ 为 $ AB $ 上一点，$ AB=4AN $，$ M$，$S $ 分别为 $ PB$，$BC $ 的中点．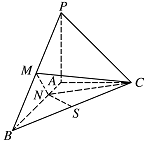
【难度】
【出处】
2010年高考辽宁卷（理）
【标注】
-
证明：$ CM\perp SN $；标注答案略解析设 $ PA=1 $，以 $ A $ 为原点，射线 $ AB$，$AC$，$AP $ 分别为 $ x$，$y$，$z $ 轴正向建立空间直角坐标系如图．
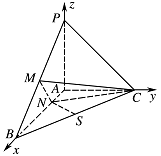则\[P\left(0,0,1\right),C\left(0,1,0\right),B\left(2,0,0\right),M\left(1,0, \dfrac{1}{2} \right),N\left( \dfrac{1}{2} ,0,0\right),S\left(1, \dfrac{1}{2} ,0\right).\]所以\[\overrightarrow {CM} = \left(1, - 1,\dfrac{1}{2}\right),\overrightarrow {SN} = \left( - \dfrac{1}{2}, - \dfrac{1}{2},0\right) ,\]因为 $\overrightarrow {CM} \cdot \overrightarrow {SN} = - \dfrac{1}{2} + \dfrac{1}{2} + 0 = 0$，所以 $ CM\perp SN $． -
求 $ SN $ 与平面 $ CMN $ 所成角的大小．标注答案略解析$\overrightarrow {NC} = \left( - \dfrac{1}{2},1,0\right)$，
设 $\overrightarrow a=\left(x,y,z\right) $ 为平面 $ CMN $ 的一个法向量，
则\[{\begin{cases}
x - y + \dfrac{1}{2}z = 0, \\
- \dfrac{1}{2}x + y = 0. \\
\end{cases}}\]令 $ x = 2 $，得 $ \overrightarrow a = \left(2,1, - 2\right) $．
因为\[\left| {\cos \left\langle {\overrightarrow a,\overrightarrow {SN} } \right\rangle } \right| = \left| {\dfrac{{ - 1 - \dfrac{1}{2}}}{{3 \times \dfrac{{\sqrt 2 }}{2}}}} \right| = \dfrac{{\sqrt 2 }}{2},\]所以 $ SN $ 与平面 $ CMN $ 所成角为 $ 45^\circ $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
