如图，在四棱锥 $S-ABCD$ 中，底面 $ABCD$ 为直角梯形，$\angle ADC=\angle BCD=90^\circ$，$BC=CD=2AD=2$，顶点 $S$ 在底面的射影 $O$ 为 $\triangle ABC$ 的重心．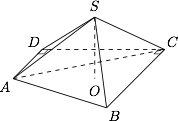
【难度】
【出处】
无
【标注】
-
若点 $P$ 在线段 $SA$ 上，且 $OP\parallel SBC$，求 $\dfrac{AP}{AS}$；标注答案$\dfrac 23$解析如图，取 $BC$ 中点 $M$，连接 $AM,SM$．
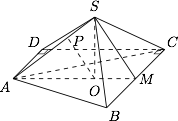根据线面平行的性质定理，有 $OP\parallel SM$，于是\[\dfrac{AP}{AS}=\dfrac{AO}{AM}=\dfrac 23.\] -
若 $SA\perp SBC$，求平面 $SAD$ 与平面 $SAC$ 所成角的余弦值．标注答案$ \dfrac{\sqrt{21}}7$解析以 $OM$ 为 $y$ 轴正方向，$OS$ 为 $z$ 轴正方向建立空间直角坐标系，则\[O(0,0,0),A\left(0,-\dfrac 43,0\right),D\left(-1,-\dfrac 43,0\right),M\left(0,\dfrac 23,0\right),S(0,0,x),\]根据题意，设 $D-SA-C$ 的大小为 $\theta$，则有\[\overrightarrow{SA}\cdot \overrightarrow{SM}=0,\]即\[\left(0,-\dfrac 43,-x\right)\cdot \left(0,\dfrac 23,-x\right)=0,\]解得\[x=\dfrac 89.\]于是\[\left\{\begin{split} D\left(-1,-\dfrac 43,0\right),\\ S\left(0,0,\dfrac{2\sqrt 2}3\right),\\ A\left(0,-\dfrac 43,0\right),\\ C\left(-1,\dfrac 23,0\right),\end{split}\right.\Rightarrow\left\{\begin{split} \overrightarrow{DS}&=\left(1,\dfrac 43,\dfrac{2\sqrt 2}3\right),\\
\overrightarrow{SA}&=\left(0,-\dfrac 43,-\dfrac{2\sqrt 2}3\right),\\
\overrightarrow{AC}&=\left(-1,-2,0\right),
\end{split}\right.\Rightarrow \left\{\begin{split} \overrightarrow n_{DSA}&=\left(0,\dfrac{2\sqrt 2}3,-\dfrac 43\right),\\
\overrightarrow n_{SAC}&=\left(-\dfrac{4\sqrt 2}3,\dfrac{2\sqrt 2}3,-\dfrac 43\right), \end{split}\right.\]于是\[\cos\theta=\sqrt{\dfrac 37},\]因此所求平面 $SAD$ 与平面 $SAC$ 所成角的余弦值为 $ \dfrac{\sqrt{21}}7$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
