如图，已知椭圆 ${C_1}$ 的中心在原点 $O$，长轴左、右端点 $M,N$ 在 $x$ 轴上，椭圆 ${C_2}$ 的短轴为 $MN$，且 ${C_1},{C_2}$ 的离心率都为 $e$．直线 $l \perp MN$，$l$ 与 ${C_1}$ 交于两点，与 ${C_2}$ 交于两点，这四点按纵坐标从大到小依次为 $A,B,C,D$．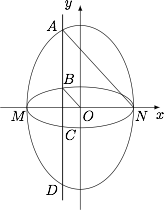
【难度】
【出处】
2011年高考辽宁卷（理）
【标注】
-
设 $e = \dfrac{1}{2}$，求 $|BC|$ 与 $|AD|$ 的比值；标注答案$\dfrac 34$解析设 $MN=2a$，则椭圆 $C_1:\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2(1-e^2)}=1$；
椭圆 $C_2:\dfrac{x^2}{a^2}+\dfrac{y^2}{\dfrac{a^2}{1-e^2}}$；所以$$\dfrac{|BC|}{|AD|}=\sqrt{\dfrac{a^2(1-e^2)}{\dfrac{a^2}{1-e^2}}}=1-e^2=\dfrac 34.$$ -
当 $e$ 变化时，是否存在直线 $l$，使得 $BO\parallel AN$，并说明理由．标注答案当 $0<e\leqslant \dfrac{\sqrt 2}{2}$ 时，不存在；当 $e>\dfrac{\sqrt 2}{2}$ 时，存在解析对椭圆 $C_1$ 作伸缩变换\[\begin{cases}x=x'\\ \dfrac{y}{\sqrt{1-e^2}}=y',\end{cases}\]则 $C_1':x^2+y^2=a^2$；
对椭圆 $C_2$ 作伸缩变换\[\begin{cases}x=x'\\ \dfrac{y}{\dfrac{1}{\sqrt{1-e^2}}}=y',\end{cases}\]则 $C_2':x^2+y^2=a^2$．
因为 $BO\parallel AN$，所以 $k_{BO}=k_{AN}$，因此\[\sqrt{1-e^2}\cdot k_{EO}=\dfrac{1}{\sqrt{1-e^2}}\cdot k_{EN},\]故\[\dfrac{k_{EO}}{k_{EN}}=\dfrac{1}{1-e^2}.\]设点 $E(a\cos \theta,a\sin \theta)$，其中 $\dfrac{\pi}{2}<\theta<\pi$，则 $k_{EO}=\dfrac{\sin \theta}{\cos \theta}$，$k_{EN}=\dfrac{\sin \theta}{\cos \theta -1}$，进而\begin{align*}
\dfrac{1}{1-e^2}
&=\dfrac{k_{EO}}{k_{EN}}\\
&=\dfrac{\cos \theta -1}{\cos \theta}\\
&>2,
\end{align*}所以当 $0<e\leqslant \dfrac{\sqrt 2}{2}$ 时，不存在；当 $\dfrac{\sqrt 2}{2}<e<1$ 时，存在．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
