如图,在矩形 $ABCD$ 中,点 $E,F$ 分别在线段 $AB、AD$ 上,$AE = EB = AF = \dfrac{2}{3}FD = 4$.沿直线 $EF$ 将 $\triangle AEF$ 翻折成 $\triangle {A'}EF$,使 $平面 {A'}EF \perp平面 BEF$.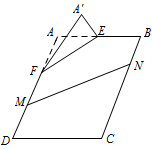

【难度】
【出处】
2010年高考浙江卷(理)
【标注】
-
求二面角 ${A'} - FD - C$ 的余弦值;标注答案略解析方法一:取线段 $ EF $ 的中点 $ H $,连接 $A'H$,
因为 $A'E = A'F$ 及 $ H $ 是 $ EF $ 的中点,所以 $A'H \perp EF$.
又因为 $平面 A'EF \perp 平面BEF$,及 $A'H \subset 平面 A'EF$.
所以 $A'H \perp平面 BEF$.
如图建立空间直角坐标系 $A - xyz$.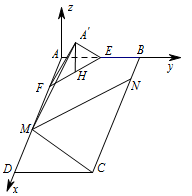 则 $A'\left(2,2,2\sqrt 2 \right)$,$C\left(10,8,0\right)$,$F\left(4,0,0\right)$,$D\left(10,0,0\right)$,则\[\overrightarrow {FA'} = \left( - 2,2,2\sqrt 2 \right),\overrightarrow {FD} = \left(6,0,0\right).\]设 $\overrightarrow n = \left(x,y,z\right)$ 为 平面 $ A'FD$ 的一个法向量,所以\[{\begin{cases}
则 $A'\left(2,2,2\sqrt 2 \right)$,$C\left(10,8,0\right)$,$F\left(4,0,0\right)$,$D\left(10,0,0\right)$,则\[\overrightarrow {FA'} = \left( - 2,2,2\sqrt 2 \right),\overrightarrow {FD} = \left(6,0,0\right).\]设 $\overrightarrow n = \left(x,y,z\right)$ 为 平面 $ A'FD$ 的一个法向量,所以\[{\begin{cases}
- 2x + 2y + 2\sqrt 2 z = 0, \\
6x = 0 ,\\
\end{cases}}\]取 $z = \sqrt 2 $,则\[\overrightarrow n = \left(0, - 2,\sqrt 2 \right),\]又平面 $ BEF $ 的一个法向量 $\overrightarrow m = \left(0,0,1\right)$,则\[\cos \left \langle \overrightarrow n ,\overrightarrow m \right \rangle = \dfrac{\overrightarrow n \cdot \overrightarrow m }{ \left|\overrightarrow n \right | \cdot \left |\overrightarrow m \right|} = \dfrac{\sqrt 3 }{3}.\]所以二面角 $A'-FD-C$ 的余弦值为 $\dfrac{\sqrt 3 }{3}.$
方法二:如图,取线段 $ EF $ 的中点 $ H $,$ AF $ 的中点 $ G $,连接 $A'H$,$ A'G $,$ GH $,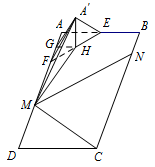 因为 $A'E = A'F$ 及 $ H $ 是 $ EF $ 的中点,所以 $A' H\perp EF$.
因为 $A'E = A'F$ 及 $ H $ 是 $ EF $ 的中点,所以 $A' H\perp EF$.
又因为 $平面 A' EF \perp 平面 BEF$,所以 $A' H\perp 平面 BEF$.
又 $AF \subset 平面 BEF$,所以 $A'H \perp AF$.
又因为 $ G $、$ H $ 分别是 $ AF $、$ EF $ 的中点,
易知 $ GH\parallel AB $,所以 $GH \perp AF$,于是 $AF \perp 面 A' GH$,
所以 $\angle A'GH$ 为二面角 $A'-DF-C$ 的平面角,
在 ${\mathrm{Rt}}\triangle A'GH$ 中,$A'H = 2\sqrt 2 $,$GH = 2$,$A'G = 2\sqrt 3 $,
所以\[\cos \angle A'GH = \dfrac{\sqrt 3 }{3},\]故二面角 $A' -DF-C$ 的余弦值为 $\dfrac{\sqrt 3 }{3}$. -
点 $M,N$ 分别在线段 $FD、BC$ 上,若沿直线 $MN$ 将四边形 $MNCD$ 向上翻折,使 $C$ 与 ${A'}$ 重合,求线段 $FM$ 的长.标注答案略解析方法一:设 $FM = x$,则 $M\left(4 + x,0,0\right)$.
因为翻折后,$ C $ 与 $ A' $ 重合,所以 $CM= A'M$,则\[{\left(6 - x\right)^2} + {8^2} + {0^2} = {\left( - 2 - x\right)^2} + {2^2} + {\left(2\sqrt 2 \right)^2},\]解得\[x = \dfrac{21}{4}.\]经检验,此时点 $ N $ 在线段 $ BC $ 上,
所以 $FM = \dfrac{21}{4}$.
方法二:连接 $MH$,设 $FM = x$,
因为翻折后,$ C $ 与 $A'$ 重合,所以 $CM = A'M$,而\[\begin{split}C{M^2} &= D{C^2} + D{M^2} \\&= {8^2} + {\left(6 - x\right)^2},\\A'{M^2} &= A'{H^2} + M{H^2} \\&= A'{H^2} + M{G^2} + G{H^2} \\&= {\left(2\sqrt 2 \right)^2} + {\left(x + 2\right)^2} + {2^2},\end{split}\]解得\[x = \dfrac{21}{4}.\]经检验,此时点 $ N $ 在线段 $ BC $ 上,
所以 $FM = \dfrac{21}{4}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2