如图,在三棱台 $ABC-DEF$ 中,已知 $ 平面 BCFE\perp 平面 ABC$,$\angle ACB=90^\circ$,$BE=EF=FC=1$,$BC=2$,$AC=3$.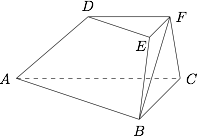

【难度】
【出处】
2016年高考浙江卷(理)
【标注】
-
求证:$BF\perp 平面 ACFD$;标注答案略解析本题的关键在于把棱台还原为棱锥,然后结合已知条件来证明.延长 $AD$,$BE$,$CF$ 相交于一点 $K$,如图所示.
 因为平面 $BCFE\perp 平面 ABC$,且 $AC\perp BC$,
因为平面 $BCFE\perp 平面 ABC$,且 $AC\perp BC$,
所以 $AC\perp 平面 BCK$,因此 $BF\perp AC$.
又因为 $EF\parallel BC$,$BE=EF=FC=1$,$BC=2$,
所以 $\triangle BCK$ 为等边三角形,且 $F$ 为 $CK$ 的中点,则 $BF\perp CK$.
所以 $BF\perp 平面 ACFD$. -
求二面角 $B-AD-F$ 的平面角的余弦值.标注答案$\dfrac{\sqrt{3}}{4}$解析如图,延长 $AD$,$BE$,$CF$ 相交于一点 $K$,则 $\triangle BCK$ 为等边三角形.
取 $BC$ 的中点 $O$,则 $KO\perp BC$,又平面 $BCFE\perp 平面 ABC$,所以 $KO\perp 平面 ABC$.
以点 $O$ 为原点,分别以射线 $OB$,$OK$ 的方向为 $x$,$z$ 轴的正方向,建立空间直角坐标系 $Oxyz$.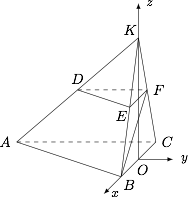 由题意得\[\begin{split}&B\left(1,0,0\right),C\left(-1,0,0\right),K\left(0,0,\sqrt 3\right),\\&A\left(-1,-3,0\right),E\left(\dfrac 12,0,\dfrac{\sqrt 3}2\right),F\left(-\dfrac 12,0,\dfrac{\sqrt 3}2\right).\end{split}\]因此\[\overrightarrow{AC}=\left(0,3,0\right),\overrightarrow{AK}=\left(1,3,\sqrt 3\right),\overrightarrow{AB}=\left(2,3,0\right).\]设平面 $ACK$ 的法向量为 $\overrightarrow m=\left(x_1,y_1,z_1\right)$,平面 $ABK$ 的法向量为 $\overrightarrow n=\left(x_2,y_2,z_2\right)$.
由题意得\[\begin{split}&B\left(1,0,0\right),C\left(-1,0,0\right),K\left(0,0,\sqrt 3\right),\\&A\left(-1,-3,0\right),E\left(\dfrac 12,0,\dfrac{\sqrt 3}2\right),F\left(-\dfrac 12,0,\dfrac{\sqrt 3}2\right).\end{split}\]因此\[\overrightarrow{AC}=\left(0,3,0\right),\overrightarrow{AK}=\left(1,3,\sqrt 3\right),\overrightarrow{AB}=\left(2,3,0\right).\]设平面 $ACK$ 的法向量为 $\overrightarrow m=\left(x_1,y_1,z_1\right)$,平面 $ABK$ 的法向量为 $\overrightarrow n=\left(x_2,y_2,z_2\right)$.
由\[\begin{cases}\overrightarrow{AC}\cdot \overrightarrow m=0,\\\overrightarrow{AK}\cdot \overrightarrow m=0\end{cases}\]得\[\begin{cases}3y_1=0,\\x_1+3y_1+\sqrt 3z_1=0,\end{cases}\]取 $\overrightarrow m=\left(\sqrt 3,0,-1\right)$;
由\[\begin{cases}\overrightarrow{AB}\cdot \overrightarrow n=0,\\\overrightarrow{AK}\cdot \overrightarrow n=0\end{cases}\]得\[\begin{cases}2x_2+3y_2=0,\\x_2+3y_2+\sqrt 3z_2=0,\end{cases}\]取 $\overrightarrow n=\left(3,-2,\sqrt 3\right)$.
于是\[\cos\langle\overrightarrow m,\overrightarrow n\rangle=\dfrac{\overrightarrow m\cdot \overrightarrow n}
{\left|\overrightarrow m\right|\cdot \left|\overrightarrow n\right|}=\dfrac{\sqrt 3}4.\]所以二面角 $B-AD-F$ 的平面角的余弦值为 $\dfrac{\sqrt 3}4$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2