如图,一个小球从 $ M $ 处投入,通过管道自上而下落到 $ A $ 或 $ B $ 或 $ C $.已知小球从每个叉口落入左右两个管道的可能性是相等的.某商家按上述投球方式进行促销活动,若投入的小球落到 $ A $、$ B $、$ C $,则分别设为 $ 1、2、3 $ 等奖.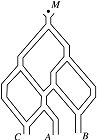

【难度】
【出处】
2010年高考浙江卷(理)
【标注】
-
已知获得 $ 1,2,3 $ 等奖的折扣率分别为 $ 50\% $、$ 70\% $、$ 90\% $.记随变量 $\xi $ 为获得 $ k\left(k=1,2,3\right) $ 等奖的折扣率,求随机变量 $\xi $ 的分布列及期望 $E\xi $;标注答案$\xi$ 的分布列为\[ \begin{array}{|c|c|c|c|} \hline
\xi&50\%&70\%&90\%\\ \hline
P&\dfrac3{16}&\dfrac38&\dfrac7{16}\\ \hline
\end{array} \]期望 $E\xi=\dfrac34$解析先找到小球落入各位置的路径,再计算相应路径的概率即可,需弄清题意.由题意,小球落入 $A $ 的概率为\[\left(\dfrac 12\right)^3+\left( \dfrac 12\right)^4= \dfrac3{16},\]即 $ P\left(\xi =50\%\right)=\dfrac3{16} $.
同理可得 $ P\left(\xi =70\%\right)=\dfrac3{8} $,$ P\left(\xi =90\%\right)=\dfrac7{16} $.
所以 $\xi$ 的分布列为\[ \begin{array}{|c|c|c|c|} \hline
\xi&50\%&70\%&90\%\\ \hline
P&\dfrac3{16}&\dfrac38&\dfrac7{16}\\ \hline
\end{array} \]则\[E\xi=\dfrac3{16}\times50\%+\dfrac38\times70\%+\dfrac7{16}\times90\%=\dfrac34.\] -
若有 $ 3 $ 人次(投入 $ 1 $ 球为 $ 1 $ 人次)参加促销活动,记随机变量 $\eta $ 为获得 $ 1 $ 等奖或 $ 2 $ 等奖的人次,求 $P\left(\eta = 2\right)$.标注答案$P\left(\eta=2\right)=\dfrac{1701}{4096}$解析随机变量 $\eta $ 服从二项分布.由(1)知,获得 $ 1 $ 等奖或 $ 2 $ 等奖的概率为\[\dfrac3{16}+\dfrac38=\dfrac9{16}.\]由题意得 $\eta~B\left(3,\dfrac9{16}\right)$,则\[P\left(\eta=2\right)={\mathrm{C}}_3^2\left(\dfrac9{16}\right)^2\left(1-\dfrac9{16}\right)=\dfrac{1701}{4096}.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2