如图，在三棱台 $ABC-DEF$ 中，$ 平面 BCFE\perp 平面 ABC$，$\angle ACB=90^\circ$，$BE=EF=FC=1$，$BC=2$，$AC=3$．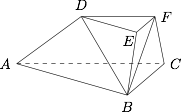
【难度】
【出处】
2016年高考浙江卷（文）
【标注】
-
求证：$BF\perp 平面 ACFD$；标注答案略解析本题的关键在于把棱台还原为棱锥，然后利用已知条件证明即可．延长 $AD$，$BE$，$CF$ 相交于一点 $K$，如图所示．
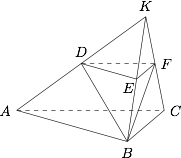因为平面 $BCFE\perp 平面 ABC$，且 $AC\perp BC$，
所以 $AC\perp 平面 BCK$，因此 $BF\perp AC$．
又因为 $EF\parallel BC$，$BE=EF=FC=1$，$BC=2$，
所以 $\triangle BCK$ 为等边三角形，且 $F$ 为 $CK$ 的中点，则 $BF\perp CK$．
所以 $BF\perp 平面 ACFD$． -
求直线 $BD$ 与平面 $ACFD$ 所成角的余弦值．标注答案$\dfrac{\sqrt{21}}7$解析本题考查线面角，先利用垂直构造出角，然后结合边长计算即可．因为 $BF\perp 平面 ACK$，所以 $\angle BDF$ 是直线 $BD$ 与平面 $ACFD$ 所成的角．
在 $\mathrm{Rt}\triangle BFD$ 中，$BF=\sqrt 3$，$DF=\dfrac 32$，得\[\cos \angle BDF=\dfrac{\sqrt{21}}7.\]所以，直线 $BD$ 与平面 $ACFD$ 所成角的余弦值为 $\dfrac{\sqrt{21}}7$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
