如图,在 $\triangle {ABC}$ 中,$\angle {ABC}=90^{\circ}$,$BD \perp AC$,$D$ 为垂足,$E$ 是 $BC$ 的中点.
求证:$\angle {EDC}=\angle {ABD}$.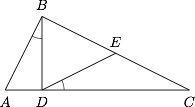
求证:$\angle {EDC}=\angle {ABD}$.

【难度】
【出处】
2016年高考江苏卷
【标注】
-
标注答案略解析利用同角的余角相等进行证明.由 $BD\perp AC$,可得 $\angle BDC=90{}^\circ $.
由 $E$ 是 $BC$ 中点,可得 $DE=CE=\dfrac{1}{2}BC$.
则 $\angle EDC=\angle C$.
由 $\angle BDC=90{}^\circ $,可得 $\angle C+\angle DBC=90{}^\circ $.
由 $\angle ABC=90{}^\circ $,可得 $\angle ABD+\angle DBC=90{}^\circ $.
因此 $\angle ABD=\angle C$.
又 $\angle EDC=\angle C$,可得 $\angle EDC=\angle ABD$.
题目
问题1
答案1
解析1
备注1