某儿童乐园在“六一”儿童节推出了一项趣味活动．参加活动的儿童需转动如图所示的转盘两次，每次转动后，待转盘停止转动时，记录指针所指区域中的数．设两次记录的数分别为 $x$，$y$．奖励规则如下：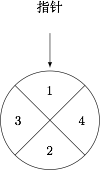
① 若 $xy\leqslant 3$，则奖励玩具一个；
② 若 $xy\geqslant 8$，则奖励水杯一个；
③ 其余情况奖励饮料一瓶．
假设转盘质地均匀，四个区域划分均匀．小亮准备参加此项活动．
① 若 $xy\leqslant 3$，则奖励玩具一个；② 若 $xy\geqslant 8$，则奖励水杯一个；
③ 其余情况奖励饮料一瓶．
假设转盘质地均匀，四个区域划分均匀．小亮准备参加此项活动．
【难度】
【出处】
2016年高考山东卷（文）
【标注】
-
求小亮获得玩具的概率；标注答案$ \dfrac{5}{16} $解析本小问考查了古典概型，需要准确写出基本事件空间与基本事件．用数对 $\left(x,y\right)$ 表示儿童参加活动先后记录的数，则基本事件空间 $\Omega$ 与点集 $S=\left\{\left(x,y\right)\left|\right.x\in\mathbb N,y\in\mathbb N,1\leqslant x\leqslant 4,1\leqslant y\leqslant 4\right\}$ 一一对应．
因为 $S$ 中的元素的个数是 $4\times 4=16$，所以基本事件总数 $n=16$．
记“$xy\leqslant 3$”为事件 $A$，则事件 $A$ 包含的基本事件数共 $5$ 个，即\[\left(1,1\right),\left(1,2\right),\left(1,3\right),\left(2,1\right),\left(3,1\right).\]所以\[P\left(A\right)=\dfrac{5}{16},\]即小亮获得玩具的概率为 $\dfrac{5}{16}$． -
请比较小亮获得水杯与获得饮料的概率大小，并说明理由．标注答案小亮获得水杯的概率大于获得饮料的概率解析本小问考查了古典概型，与 $(1)$ 问大致相同．记“$xy\geqslant 8$”为事件 $B$，“$3<xy<8$”为事件 $C$．则事件 $B$ 包含的基本事件数共 $6$ 个，即\[\left(2,4\right),\left(3,3\right),\left(3,4\right),\left(4,2\right),\left(4,3\right),\left(4,4\right).\]所以\[P\left(B\right)\overset{\left[a\right]}=\dfrac{6}{16}=\dfrac{3}{8},\]事件 $C$ 包含的基本事件数共 $5$ 个，即\[\left(1,4\right),\left(2,2\right),\left(2,3\right),\left(3,2\right),\left(4,1\right).\]所以\[P\left(C\right)=\dfrac{5}{16}.\]因为 $\dfrac{3}{8}>\dfrac{5}{16}$，所以小亮获得水杯的概率大于获得饮料的概率．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
