在如图所示的几何体中，$D$ 是 $AC$ 的中点，$EF\parallel DB$．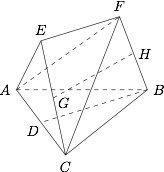
【难度】
【出处】
2016年高考山东卷（文）
【标注】
-
已知 $AB=BC$，$AE=EC$．求证：$AC\perp FB$；标注答案略解析因为 $EF\parallel DB$，
所以 $EF$ 与 $DB$ 确定平面 $BDEF$．
连接 $DE$．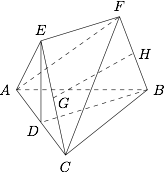
因为 $AE=EC$，$D$ 为 $AC$ 的中点，
所以 $DE\perp AC$．
同理可得 $BD\perp AC$．
又 $BD\cap DE=D$，
所以 $AC\perp$ 平面 $BDEF$．
因为 $FB\subset$ 平面 $BDEF$，
所以 $AC\perp FB$． -
已知 $G,H$ 分别是 $EC$ 和 $FB$ 的中点．求证：$GH\parallel $ 平面 $ABC$．标注答案略解析本小问考查线面平行，要证线面平行，则一般可以通过构造中位线，平行四边形利用线面平行的判定定理证，或者构造平面，利用面面平行的性质定理证明．设 $FC$ 的中点为 $I$，连接 $GI$，$HI$．
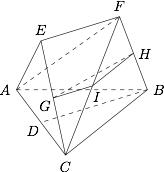在 $\triangle CEF$ 中，因为 $G$ 是 $CE$ 的中点，
所以 $GI\parallel EF$，
又 $EF\parallel DB$，
所以 $GI\parallel DB$，
在 $\triangle CFB$ 中，因为 $H$ 是 $FB$ 的中点，
所以 $HI\parallel B C$，
又 $HI\cap GI=I$，
所以平面 $GHI\parallel$ 平面 $ABC$．
因为 $GH\subset $ 平面 $GHI$，
所以 $GH\parallel$ 平面 $ABC$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
