已知 $ m $ 是非零实数,抛物线 $ C:y^2=2px\left(p>0\right) $ 的焦点 $ F $ 在直线 $ l:x-my-{\dfrac{m^2}{2}}=0 $ 上.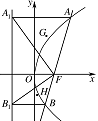

【难度】
【出处】
2010年高考浙江卷(文)
【标注】
-
若 $ m=2 $,求抛物线 $ C $ 的方程;标注答案略解析由焦点 $ F \left({\dfrac{p}{2}},0\right) $ 在直线 $ l $ 上,得\[ p=m^2 ,\]又 $ m=2 $,则\[p=4.\]所以抛物线 $ C $ 的方程为\[ y^2=8x .\]
-
设直线 $ l $ 与抛物线 $ C $ 交于 $ A $、$ B $ 两点,过 $ A $、$ B $ 分别作抛物线 $ C $ 的准线的垂线,垂足分别为 $ A_1 $、$ B_1 $,$ \triangle AA_1F $、$ \triangle BB_1F $ 的重心分别为 $ G $、$ H $.求证:对任意非零实数 $ m $,抛物线 $ C $ 的准线与 $ x $ 轴的交点在以线段 $ GH $ 为直径的圆外.标注答案略解析由(1)得 $ p=m^2 $,则抛物线 $ C $ 的方程为\[ y^2=2m^2x. \]设 $ A\left(x_1,y_1\right) $,$ B\left(x_2,y_2\right) $,由\[ \begin{cases}x=my+{\dfrac{m^2}{2}},\\ y^2=2m^2x ,\end{cases}\]消去 $ x $ 得\[ y^2-2m^3y-m^4=0,\]由于 $ m\neq 0 $,则\[ \Delta =4m^6+4m^4>0,\]且有\[ y_1+y_2=2m^3,y_1y_2=-m^4.\]设 $ M_1 $、$ M_2 $ 分别为线段 $ AA_1 $、$ BB_1 $ 的中点,
由于 $ 2{\overrightarrow {M_1G}}={\overrightarrow {GF}} $,$ 2{\overrightarrow {M_2H}}={\overrightarrow {HF}} $,可知\[ G \left({\dfrac{x_1}{3}} , {\dfrac{2y_1}{3}}\right),H\left( {\dfrac{x_2}{3}}, {\dfrac{2y_2}{3}}\right), \]则\[ \begin{split}& {\dfrac{x_1+x_2}{6}}={\dfrac{m\left(y_1+y_2\right)+m^2}{6}}={\dfrac{m^4}{3}}+{\dfrac{m^2}{6}},\\ &{\dfrac{2y_1+2y_2}{6}}={\dfrac{2m^3}{3}}, \end{split}\]所以 $ GH $ 的中点为\[ M \left({\dfrac{m^4}{3}}+{\dfrac{m^2}{6}},{\dfrac{2m^3}{3}}\right). \]设 $ R $ 是以线段 $ GH $ 为直径的圆的半径,则\[ R^2={\dfrac{1}{4}}|GH|^2={\dfrac{1}{9}}\left(m^2+4\right)\left(m^2+1\right)m^4. \]而抛物线的准线与 $ x $ 轴交点为 $ N\left( -{\dfrac{m^2}{2}},0 \right) $,则\[\begin{split} |MN|^2 &= \left({\dfrac{m^2}{2}}+{\dfrac{m^4}{3}}+{\dfrac{m^2}{6}}\right)^ 2+ \left({\dfrac{2m^3}{3}}\right)^ 2\\&={\dfrac{1}{9}}m^4\left(m^4+8m^2+4\right)\\&={\dfrac{1}{9}}m^4\left[\left(m^2+1\right)\left(m^2+4\right)+3m^2\right]\\&>{\dfrac{1}{9}}m^4\left(m^2+1\right)\left(m^2+4\right)\\&=R^2, \end{split}\]故 $ N $ 在以线段 $ GH $ 为直径的圆外.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2