如图，在平行四 边形 $ ABCD $ 中，$ AB=2BC $，$ \angle ABC=120^\circ $，$ E $ 为线段 $ AB $ 的中点，将 $ \triangle ADE $ 沿直线 $ DE $ 翻折成 $ \triangle A′DE $，使 $ 平面 A′DE\perp 平面 BCD $，$ F $ 为线段 $ A′C $ 的中点．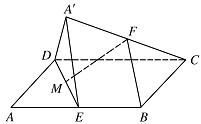
【难度】
【出处】
2010年高考浙江卷（文）
【标注】
-
求证：$ BF\parallel 平面 A′DE $；标注答案略解析如图所示，取 $ A′D $ 的中点 $ G $，连接 $ GF $，$ GE $，
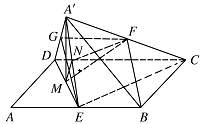由条件易知 $ FG\parallel CD $，$ FG={\dfrac{1}{2}}CD $，$ BE\parallel CD $，$ BE={\dfrac{1}{2}}CD $，
所以 $ FG\parallel BE $，$ FG=BE $，则四边形 $ BEGF $ 为平行四边形，所以 $ BF\parallel EG $．
因为 $ EG \subset 平面 A′DE $，$ BF \not\subset平面 A′DE $，
所以 $ BF\parallel 平面 A′DE $． -
设 $ M $ 为线段 $ DE $ 的中点，求直线 $ FM $ 与平面 $ A′DE $ 所成角的余弦值．标注答案略解析在平行四边形 $ ABCD $ 中，设 $ BC=a $，则\[\begin{split}AB&=CD=2a, \\ AD&=AE=EB=a ,\end{split}\]连接 $ CE $，因为 $ \angle ABC=120^\circ $，
在 $ \triangle BCE $ 中，由余弦定理可得 $ CE={\sqrt{3}}a $，
在 $ \triangle ADE $ 中，可得 $ DE=a $，
又 $ CD=2a$，所以 $ CD^2=CE^2+DE^2 $，从而 $ CE\perp DE $，
在正三角形 $ A′DE $ 中，$ M $ 为 $ DE $ 中点，所以 $ A′M\perp DE $．
由 $ 平面 A′DE\perp 平面 BCD $，
可知 $ A′M\perp 平面 BCD $，从而 $ A′M\perp CE $．
又 $A'M\cap DE=M $，所以 $ CE\perp 平面 A'DE$，
取 $ A′E $ 的中点 $ N $，连接 $ NM $，$ NF $，则 $NF\parallel CE $，
所以 $ NF\perp 平面 A′DE $，
则 $ \angle FMN $ 为直线 $ FM $ 与平面 $ A′DE $ 所成角．
在 $ {\mathrm{Rt}}\triangle FMN $ 中，$ NF={\dfrac{{\sqrt{3}}}{2}}a $，$ MN={\dfrac{1}{2}}a $，$ FM=a $，则\[ \cos \angle FMN={\dfrac{1}{2}}, \]所以直线 $ FM $ 与平面 $ A′DE $ 所成角的余弦值为 $ {\dfrac{1}{2}} $．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
