如图所示,为了制作一个圆柱形灯笼,先要制作 $ 4 $ 个全等的矩形骨架,总计耗用 $ 9.6 $ 米铁丝,再用 $S$ 平方米塑料片制成圆柱的侧面和下底面(不安装上底面).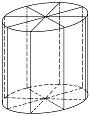

【难度】
【出处】
2010年高考上海卷(文)
【标注】
-
当圆柱底面半径 $r$ 取何值时,$S$ 取得最大值?并求出该最大值(结果精确到 $ 0.01 $ 平方米);标注答案略解析圆柱体的高为 $1.2 - 2r$,故\[\begin{split}S = {\mathrm \pi } {r^2} + 2{\mathrm \pi }r\left(1.2 - 2r\right) ={\mathrm \pi } \left( - 3{r^2} + 2.4r\right)\left(0<r<0.6\right).\end{split}\]当 $r = 0.4$ 时,\[{S_{\max }} = 1.5080 \approx 1.51\left({{\mathrm{m}}^2}\right).\]
-
若要制作一个如图放置的,底面半径为 $ 0.3 $ 米的灯笼,请作出用于灯笼的三视图(作图时,不需考虑骨架等因素).标注答案略解析当 $ r=0.3 $ 时,$ l=0.6 $,作三视图如图.
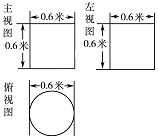
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2