如图所示，为了制作一个圆柱形灯笼，先要制作 $ 4 $ 个全等的矩形骨架，总计耗用 $ 9.6 $ 米铁丝．骨架将圆柱底面 $ 8 $ 等分．再用 $ S $ 平方米塑料片制成圆柱的侧面和下底面（不安装上底面）．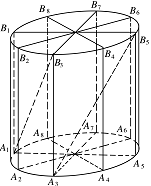
【难度】
【出处】
2010年高考上海卷（理）
【标注】
-
当圆柱底面半径 $ r $ 取何值时，$ S $ 取得最大值？并求出该最大值（结果精确到 $ 0.01 $ 平方米）；标注答案略解析设圆柱形灯笼的母线长为 $ l $，则\[\begin{split} l&=1.2-2r\left(0<r<0.6\right) ,\\ S&=-3{\mathrm \pi }\left(r-0.4\right)^2+0.48{\mathrm \pi },\end{split}\]所以当 $ r=0.4 $ 时，$ S $ 取得最大值约为 $ 1.51 $ 平方米．
-
在灯笼内，以矩形骨架的顶点为端点，安装一些霓虹灯．当灯笼底面半径为 $ 0.3 $ 米时，求图中两根直线型霓虹灯 $ A_{1}B_{3} $、$ A_{3}B_{5} $ 所在异面直线所成角的的余弦值．标注答案略解析当 $ r=0.3 $ 时，$ l=0.6 $，建立空间直角坐标系，
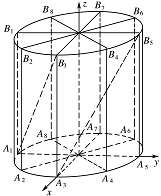可得 $\overrightarrow {{A_1}{B_3}} = \left( 0.3,0.3,0.6\right)$，$\overrightarrow {{A_3}{B_5}} = \left( - 0.3, 0.3,0.6\right)$，
设向量 $\overrightarrow {{A_1}{B_3}} $ 与 $\overrightarrow {{A_3}{B_5}} $ 的夹角为 $\theta $，则\[\cos \theta = \dfrac{{\overrightarrow {{A_1}{B_3}} \cdot \overrightarrow {{A_3}{B_5}} }}{{ \left|\overrightarrow {{A_1}{B_3}} \right| \cdot \left |\overrightarrow {{A_3}{B_5}} \right|}} = \dfrac{2}{3},\]所以 $ A_{1}B_{3} $、$ A_{3}B_{5} $ 所在异面直线所成角的余弦值为 $\dfrac{2}{3}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
