如图，四棱锥 $P-ABCD$ 的底面 $ABCD$ 为平行四边形，$E,F$ 分别为 $CD,PB$ 的中点，在线段 $PC$ 上是否存在一点 $Q$，使 $A,E,Q,F$ 四点共面？若存在，求出 $\dfrac{PQ}{QC}$．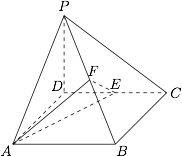
【难度】
【出处】
无
【标注】
【答案】
$2$
【解析】
如图，延长 $BC$ 至 $G$，使得 $BC=CG$，连接 $PG,EG,FG$．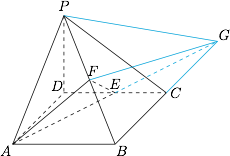
根据题意，平面 $AEF$ 即平面 $AEGF$，于是 $FG$ 为平面 $AEF$ 与平面 $PBC$ 的交线，从而 $PC$ 与 $FG$ 的交点即为所求点 $Q$．由于 $Q$ 是 $\triangle PBG$ 的重心，因此 $\dfrac{PQ}{QC}=2$．
根据题意，平面 $AEF$ 即平面 $AEGF$，于是 $FG$ 为平面 $AEF$ 与平面 $PBC$ 的交线，从而 $PC$ 与 $FG$ 的交点即为所求点 $Q$．由于 $Q$ 是 $\triangle PBG$ 的重心，因此 $\dfrac{PQ}{QC}=2$．
答案
解析
备注
