如图，椭圆 $C:\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1(a>b>0)$ 的离心率为 $\dfrac{1}{2}$，其左焦点到点 $P(2,1)$ 的距离为 $\sqrt{10}$，不过原点 $O$ 的直线 $l$ 与 $C$ 相交 $A,B$ 两点，且线段被直线 $OP$ 平分．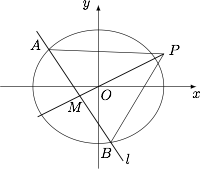
【难度】
【出处】
2012年高考浙江卷（理）
【标注】
-
求椭圆 $C$ 的方程；标注答案$\dfrac{x^{2}}{4}+\dfrac{y^{2}}{3}=1$解析设线段 $AB$ 的中点为 $M$，椭圆方程为 $\dfrac{x^{2}}{4}+\dfrac{y^{2}}{3}=c^{2}$，则左焦点 $(-c,0)$ 到点 $P(2,1)$ 的距离为\[\sqrt{(2+c)^{2}+1^{2}}=\sqrt{10},\]所以 $c=1$，从而椭圆方程为 $\dfrac{x^{2}}{4}+\dfrac{y^{2}}{3}=1$．
-
求 $\triangle APB$ 的面积取得最大值时直线 $l$ 的方程．标注答案$y=-\dfrac{3}{2}x+1-\sqrt 7$解析作仿射变换\[(x',y')=\left(x,\dfrac 2{\sqrt3}y\right),\]则 $P'\left(2,\dfrac 2{\sqrt 3}\right)$，且 $P'M'\perp A'B'$．如图：
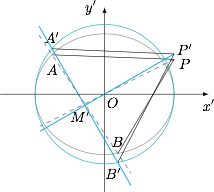设 $OM'=d$，则\[\begin{split} S_{\triangle A'P'B'}&=\dfrac 12\cdot 2A'M'\cdot P'M'\\
&=\sqrt{4-d^2}\cdot \left(\dfrac{4}{\sqrt 3}+d\right)\\
&=\sqrt{\left(4-d^2\right)\left(\dfrac 4{\sqrt 3}+d\right)^2},\end{split}\]记\[\varphi(d)=\left(4-d^2\right)\left(\dfrac 4{\sqrt 3}+d\right)^2,\]则其导函数\[\varphi'(d)=-4\left(d+\dfrac{4}{\sqrt 3}\right)\left(d^2+\dfrac 2{\sqrt 3}d-2\right),\]因此当 $d=\dfrac{\sqrt 7-1}{\sqrt 3}$ 时 $S_{\triangle A'P'B'}$ 取得最大值．考虑到直线 $P'M'$ 的倾斜角为 $\dfrac{\pi}6$，于是 $\triangle APB$ 的面积取得最大值时直线 $A'B'$ 的横截距，即直线 $AB$ 的横截距为\[-\dfrac{\sqrt 7-1}{\sqrt 3}\cdot \dfrac{2}{\sqrt 3}=\dfrac {2-2\sqrt 7}3,\]进而直线 $l$ 的方程为\[y=-\dfrac 32\left(x+\dfrac {2\sqrt 7-2}3\right),\]即\[y=-\dfrac 32x+1-\sqrt 7.\]
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
