已知抛物线 $C:{y^2}= 2px\left(p > 0\right)$ 的焦点为 $F$，$A$ 为 $C$ 上异于原点的任意一点，过点 $A$ 的直线 $l$ 交 $C$ 于另一点 $B$，交 $x$ 轴的正半轴于点 $D$，且有 $|FA| = |FD|$．当点 $A$ 的横坐标为 $3$ 时，$\triangle ADF$ 为正三角形．
【难度】
【出处】
2014年高考山东卷（理）
【标注】
-
求 $C$ 的方程；标注答案抛物线 $C$ 的方程为 $C:y^2=4x$解析因为 $|FA|=|FD|>\dfrac p2=|FO|$，所以点 $D$ 一定在 $F$ 右侧，根据题意，作出示意图．
当点 $A$ 的横坐标是 $3$ 时，不妨设其坐标为 $\left(3,\sqrt{6p}\right)$，又由于 $\triangle AFD$ 为等边三角形，因此 $A$ 点的纵坐标为 $\sqrt 3\cdot\left(3-\dfrac p2\right)$，因此$$\sqrt{6p}=\sqrt 3\cdot\left(3-\dfrac p2\right),$$解得 $p=2$，因此抛物线 $C$ 的方程为 $C:y^2=4x$． -
若直线 ${l_1}\parallel l$，且 ${l_1}$ 和 $C$ 有且只有一个公共点 $E$，
（i）证明直线 $AE$ 过定点，并求出定点坐标；
（ii）$\triangle ABE$ 的面积是否存在最小值？若存在，请求出最小值；若不存在，请说明理由．标注答案$(1)$ 直线 $AE$ 过定点 $F(1,0)$．
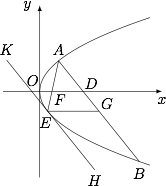
$(2)$ 三角形 $ABE$ 的面积存在最小值 $16$解析（i）过 $E$ 作 $x$ 轴的平行线，交 $AB$ 于点 $G$，将 $l_1$ 标记为 $KH$，其中点 $K$ 与 $A$ 在直线 $EG$ 的同侧，如图．由抛物线的光学性质得 $\angle FEK=\angle GEH$，又$$\angle GEH=\angle EGA=\angle FDA=\angle FAD,$$因此 $A,F,E$ 三点共线，于是直线 $AE$ 过定点 $F(1,0)$．
（ii）首先证明：引理 若抛物线 $y^2=2px$（$p>0$）与直线 $x=my+t$ 相交于点 $P(x_1,y_1)$ 和点 $Q(x_2,y_2)$，与直线 $x=my+t_0$ 相切于 $T(x_0,y_0)$，则有 $x_1x_2=t^2$，$\dfrac{y_1+y_2}2=y_0$．引理的证明 联立直线 $x=my+t$ 与抛物线的方程，可得 $y^2-2pmy-2pt=0$，从而$$x_1x_2=\dfrac{y_1^2y_2^2}{4p^2}=t^2,$$且$$\dfrac{y_1+y_2}2=pm.$$联立直线 $x=my+t_0$ 与抛物线的方程，可得 $y^2-2pm-2pt_0=0$，从而 $y_0=pm$，因此$$\dfrac{y_1+y_2}2=y_0.$$因此引理得证．
设点 $A$ 的坐标为 $\left(4t^2,4t\right)$，则由 $F(1,0)$ 以及引理可得 $E\left(\dfrac{1}{4t^2},-\dfrac 1t\right)$，又由抛物线的定义，$|DF|=|AF|=4t^2+1$，于是点 $D\left(4t^2+2,0\right)$，进而应用引理可得$$B\left(\dfrac{(4t^2+2)^2}{4t^2},-\left(4t+\dfrac 2t\right)\right),$$再由直线方程可得 $G\left(\dfrac{1}{2t^2}+4t^2+2,-\dfrac 1t\right)$，因此三角形 $ABE$ 的面积\[\begin{split}S&= \dfrac 12 |EG|\cdot |y_A-y_B|\\
&=\dfrac 12\left(4t^2+\dfrac 1{4t^2}+2\right)\cdot\left|8t+\dfrac 2t\right|\\
&=\dfrac 14\left|4t+\dfrac 1t\right|^3\\
&\geqslant \dfrac 14\cdot 4^3=16,\end{split}\]等号当且仅当 $t=\pm \dfrac 12$ 时取得．因此三角形 $ABE$ 的面积存在最小值 $16$，当 $A$ 的坐标为 $(1,\pm 2)$ 时取得．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
