已知对任意 $x\in [0,1]$,均有 $\big|ax^2+bx+c\big|\leqslant 1$,求 $\big|cx^2+bx+a\big|$ 在 $[0,1]$ 上的最大值.
【难度】
【出处】
无
【标注】
【答案】
$8$
【解析】
设 $f(x)=ax^2+bx+c$,则$$\begin{cases} f(0)=c,\\ f\left(\dfrac 12\right)=\dfrac 14a+\dfrac 12b+c,\\ f(1)=a+b+c,\end{cases}$$解得$$\begin{cases} a=2f(0)+2f(1)-4f\left(\dfrac 12\right),\\ b=4f\left(\dfrac 12\right)-3f(0)-f(1),\\ c=f(0),\end{cases}$$于是当 $x\in [0,1]$ 时,有\[\begin{split} \big|cx^2+bx+a\big|-\big|ax^2+bx+c\big|&\leqslant \big|cx^2+bx+a-(ax^2+bx+c)\big|\\ &=\big|(a-c)(1-x^2)\big| \leqslant \big|a-c\big| \\ &=\left|f(0)+2f(1)-4f\left(\dfrac 12\right)\right|\\ &\leqslant \big|f(0)\big|+2\big|f(1)\big|+4\left|f\left(\dfrac 12\right)\right| \\&\leqslant 7,\end{split}\]因此有$$\big|cx^2+bx+a\big|\leqslant 7+\big|ax^2+bx+c\big|\leqslant 8,$$事实上,取 $a=8,b=-8,c=1,x=0$ 可得 $\big|cx^2+bx+a\big|=8$,因此所求的最大值为 $8$.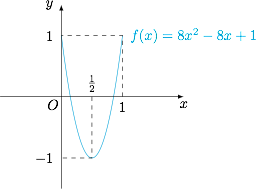

答案
解析
备注