已知长方形 $ABCD$ 中 $AB=4$,$AD=2$.$M$ 为 $DC$ 的中点,将 $\triangle ADM$ 沿 $AM$ 折起,使得平面 $ADM\perp$ 平面 $ABCM$.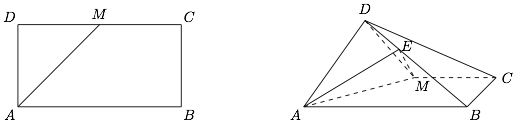

【难度】
【出处】
2017年清华大学THUSSAT测试理科数学(二测)
【标注】
-
求证:$AD\perp BM$;标注答案略解析根据题意,有\[\left.\begin{split} AM\perp BM,\\ ADM\perp ABCM,\\ AM=ADM\cap ABCM,\end{split}\right\}\Rightarrow BM\perp ADM\Rightarrow AD\perp BM.\]
-
若 $\overrightarrow{DE}=\lambda\overrightarrow{EB}$($\lambda>0$),当二面角 $E-AM-D$ 的大小为 $\dfrac{\pi}3$ 时,求 $\lambda$ 的值.标注答案$\dfrac{\sqrt 6}8$解析设未折起时 $D$ 点位置为 $O$,以 $OA,OC$ 为 $x,y$ 轴正方向建立空间直角坐标系,则\[A(2,0,0),B(2,4,0),C(0,4,0),D(1,1,\sqrt 2),M(0,2,0),E\left(\dfrac{1+2\lambda}{1+\lambda},\dfrac{1+4\lambda}{1+\lambda},\dfrac{\sqrt 2}{1+\lambda}\right),\]从而\[\begin{split}
\overrightarrow{AE}&=\left(\dfrac{-1}{1+\lambda},\dfrac{1+4\lambda}{1+\lambda},\dfrac{\sqrt 2}{1+\lambda}\right),\\
\overrightarrow{AM}&=(-2,2,0),\end{split}\]从而平面 $AEM$ 的法向量\[\overrightarrow n=(-1,-1,2\sqrt 2\lambda),\]由于二面角 $E-AM-D$ 的大小为 $\dfrac{\pi}3$,于是 $E-AM-B$ 的大小为 $\dfrac{\pi}6$,因此\[\overrightarrow n\cdot (0,0,1)=\dfrac{\sqrt 3}2,\]解得 $\lambda=\dfrac{\sqrt 6}8$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2