过抛物线 $y^2=2px$（$p>0$）外一点 $P$ 作抛物线的两条切线 $PA,PB$，求证：$\triangle PFA$ 与 $\triangle BFP$ 相似．
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
分别作 $F$ 关于 $PA,PB$ 的对称点 $A_1,B_1$，连接 $FA_1,FB_1$ 分别交 $PA,PB$ 于 $M,N$，连接 $PA_1,PB_1,A_1B_1$，$PA$ 与 $A_1B_1$ 交于点 $Q$，如图．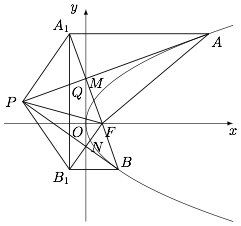
根据抛物线的光学性质，有\[AA_1\parallel BB_1\parallel OF,\]于是 $A_1B_1$ 是抛物线 $y^2=2px$ 的准线．$MN$ 是 $\triangle FA_1B_1$ 的中位线，于是 $MN\parallel$．由于 $FM\perp PA$，$PN\perp PB$，于是 $P,M,F,N$ 四点共圆，于是\[\angle BPF=\angle NMF=\angle B_1A_1F ,\]又 $Q,A_1,A,F$ 四点共圆，于是\[\angle B_1A_1F=\angle FAP,\]从而\[\angle BPF=\angle FAP,\]同理可得\[\angle APF=\angle FBP,\]因此 $\triangle PFA$ 与 $\triangle BFP$ 相似．
根据抛物线的光学性质，有\[AA_1\parallel BB_1\parallel OF,\]于是 $A_1B_1$ 是抛物线 $y^2=2px$ 的准线．$MN$ 是 $\triangle FA_1B_1$ 的中位线，于是 $MN\parallel$．由于 $FM\perp PA$，$PN\perp PB$，于是 $P,M,F,N$ 四点共圆，于是\[\angle BPF=\angle NMF=\angle B_1A_1F ,\]又 $Q,A_1,A,F$ 四点共圆，于是\[\angle B_1A_1F=\angle FAP,\]从而\[\angle BPF=\angle FAP,\]同理可得\[\angle APF=\angle FBP,\]因此 $\triangle PFA$ 与 $\triangle BFP$ 相似．
答案
解析
备注
