如图，已知四棱锥 $P - ABCD$ 的底面 $ABCD$ 是菱形，$PA \perp \text{平面} ABCD$，点 $F$ 为 $PC$ 的中点．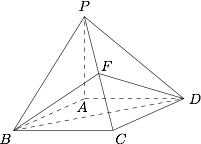
【难度】
【出处】
2013年清华大学夏令营数学试题
【标注】
-
求证：$PA\parallel$ 平面 $BDF$；标注答案略解析连接 $AC$ 交 $BD$ 于 $O$，连接 $FO$，如图．
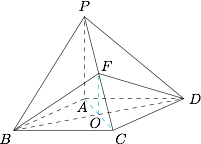由于 $OA=OC$，$FP=FC$，所以 $FO\parallel PA$，而 $PA\not\subset \text{平面}BDF$，$FO\subset \text{平面}BDF$，故 $PA\parallel \text{平面} BDF$． -
求证：平面 $PAF\perp$ 平面 $BDF$；标注答案略解析由于 $PA\perp \text{平面} ABCD$，所以 $PA\perp BD$，又 $AC\perp BD$，且 $PA\cap AC=A$，故 $BD\perp \text{平面} PAC$，又因为 $BD\subset\text{平面}BDF$，所以 $\text{平面} PAF\perp \text{平面} BDF$．
-
设 $BD = 3PA = 3AC = 3$，求三棱锥 $P - ADF$ 的体积．标注答案$\dfrac{1}{8}$解析由题意得$$\begin{split} {V_{P - ADF}} =& {V_{F - PAD}} = \dfrac{1}{2}{V_{C - PAD}} = \dfrac{1}{2}{V_{P - ACD}} \\=& \dfrac{1}{4}{V_{P - ABCD}} =\dfrac 14\cdot\dfrac 13\cdot\dfrac 12\cdot 3\cdot 1\cdot 1\\=&\dfrac{1}{8}.\end{split}$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
