设四棱锥 $P - ABCD$ 中,底面 $ABCD$ 是边长为 $1$ 的正方形,且 $PA \perp \text{平面} ABCD$.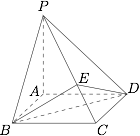

【难度】
【出处】
2004年同济大学自主招生优秀考生文化测试
【标注】
-
求证:直线 $PC \perp BD$;标注答案略解析连接 $AC$,由$$PA \perp \text{平面} ABCD,$$所以$$PA \perp BD,$$又$$AC \perp BD,PA\cap AC=A,$$所以$$BD \perp \text{平面} PAC,$$于是$$BD \perp PC.$$
-
过直线 $BD$ 且垂直于直线 $PC$ 的平面交 $PC$ 于点 $E$,如果三棱锥 $E-BCD$ 的体积取到最大值,求此时四棱锥 $P-ABCD$ 的高.标注答案$\sqrt 2$解析设 $PA = x$,$\overrightarrow {CE} = \lambda \overrightarrow {CP} $,则$$A\left( {0, 0, 0} \right) , B\left( {1, 0, 0} \right) , C\left( {1, 1, 0} \right) , D\left( {0, 1, 0} \right) , P\left( {0, 0, x} \right).$$因为 $\overrightarrow {CP} = \left( { -1,-1, x} \right)$,所以$$\overrightarrow {BE} = \overrightarrow {BC} + \overrightarrow {CE} = \left( {0, 1, 0} \right) + \lambda \left( { - 1, - 1, x} \right)=\left( { - \lambda , 1 - \lambda , \lambda x} \right),$$而 $PC \perp \text{平面} BED$,所以 $\overrightarrow {CP} \perp \overrightarrow {BE} $,于是$$\lambda + \lambda - 1 + \lambda {x^2} = 0,$$解得$$\lambda = \dfrac{1}{{{x^2} + 2}},$$故$${V_{E - BCD}} = \lambda {V_{P - BCD}} = \lambda x \cdot \dfrac{{{S_{\triangle BCD}}}}{3} = \dfrac{x}{{{x^2} + 2}} \cdot \dfrac 16 = \dfrac{1}{{x + \frac{2}{x}}} \cdot \dfrac 16,$$所以当且仅当 $x = \sqrt 2 $ 时,${V_{E - BCD}}$ 取得最大值.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2