题目 设函数 $f(x)=\begin{cases}x^2+bx+c,&x\leqslant 0,\\2,&x>0,\end{cases}$ 其中 $b>0$，$c\in \mathbb R$．当且仅当 $x=-2$ 时，函数 $f(x)$ 取得最小值 $-2$． 问题1 求函数 $f(x)$ 的表达式； 答案1 $f(x)=\begin{cases}x^2+4x+2,&x\leqslant 0,\\ 2,&x>0.\end{cases}$ 解析1 因为当且仅当 $x=-2$ 时，$f(x)$ 有最小值 $-2$，所以$$\begin{cases}-\dfrac b2 =-2,\\ 4-2b+c=-2,\end{cases}$$所以$$b=4,c=2,$$故$$f(x)=\begin{cases}x^2+4x+2,&x\leqslant 0,\\ 2,&x>0.\end{cases}$$ 备注1 问题2 若方程 $f(x)=x+a$（$a\in \mathbb R$）至少有两个不同的实数根，求 $a$ 的取值范围． 答案2 $\left[-\dfrac 14,2\right]$ 解析2 令$$g(x)=f(x)-x=\begin{cases}x^2+3x+2,&x\leqslant 0,\\ -x+2,&x>0.\end{cases}$$其图象如下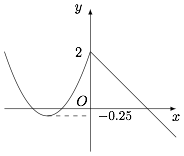．<img src="/static/images/e5b424c56db9e87c74a78f337d623e65.png" class="img-responsive" />因此若方程 $f(x)=x+a$ 至少有两个不同的实数根，则$$-\dfrac 14\leqslant a\leqslant 2.$$即 $a$ 的取值范围为 $\left[-\dfrac 14,2\right]$． 备注2