已知 $x$ 为实数,用 $[x]$ 表示不超过 $x$ 的最大整数,例如 $[1.2]=1$,$[-1.2]=-2$,$[1]=1$.对于函数 $f(x)$,若存在 $m\in\mathbb R\land m\notin\mathbb Z$,使得 $f(m)=f([m])$,则称函数 $f(x)$ 是 $\Omega$ 函数.
【难度】
【出处】
无
【标注】
-
判断函数 $f(x)=x^2-\dfrac 13x$,$g(x)=\sin\pi x$ 是否是 $\Omega$ 函数;(只需写出结论)标注答案$f(x)=x^2-\dfrac 13x$ 是 $\Omega$ 函数,$g(x)=\sin\pi x$ 不是 $\Omega$ 函数解析题中给出了取整函数对单个实数的影响,让我们研究它对函数的影响.事实上.它起到对函数取样的作用.比如,在每天的早上8点钟测量气温作为当天 $24$ 小时的气温,这种做法就可以认为是对气温的变化曲线进行抽样.
在本题中,我们考虑用 $k$ 处的函数值作为区间 $[k,k+1)$($k\in\mathbb{Z}$)上的取样,得到一个函数的抽样函数.例如,正比例函数 $f(x)=x$ 的抽样,如图1: 三次函数 $f(x) =\dfrac 14x^3-2x^2+x+8$ 的抽样,如图2:
三次函数 $f(x) =\dfrac 14x^3-2x^2+x+8$ 的抽样,如图2: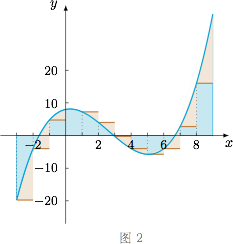 $f(x)=\sin x$ 的抽样,如图3:
$f(x)=\sin x$ 的抽样,如图3: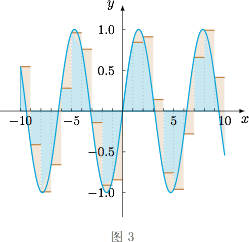 根据对抽样的理解,就可以得到 $\Omega$ 函数的判断法则:
根据对抽样的理解,就可以得到 $\Omega$ 函数的判断法则:
如果一个函数和它的抽样函数有除抽样点外的公共点,那么称之为 $\Omega$ 函数.而想要成为 $\Omega$ 函数,那么需要在某个取样周期内完成“调头”(可以借助“最小转弯半径”的概念来理解).
$(1)$ 不难发现,一个函数在单调区间上是不可能和它的抽样函数有公共点的.因此对于函数 $f(x)=x^2-\dfrac 13x$,只需要考虑其单调性发生改变,即对称轴附近的抽样区间 $[0,1)$ 即可得到结论.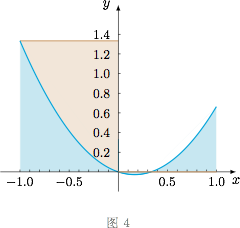 如图4,函数 $f(x)=x^2-\dfrac 13x$ 是 $\Omega$ 函数,因为 $f(1/3)=f([1/3])=0$.
如图4,函数 $f(x)=x^2-\dfrac 13x$ 是 $\Omega$ 函数,因为 $f(1/3)=f([1/3])=0$.
对函数 $g(x)=\sin \pi x$,虽然有很多单调性发生改变的地方,但是每次“调头”都需要长度为 $1$ 的区间,由于周期的限制,不是 $\Omega$ 函数,如图5.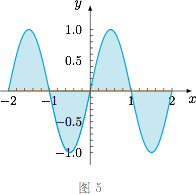
-
设函数 $f(x)$ 是定义在 $\mathbb R$ 上的周期函数,其最小正周期是 $T$,若 $f(x)$ 不是 $\Omega$ 函数,求 $T$ 的最小值;标注答案$T$ 的最小值为 $1$解析$T$ 的最小值为 $1$,证明如下.
第 $(1)$ 小题提示我们构造出 $T=1$ 的例子$$f(x)=\sin{\pi x},$$因此只需要证明当 $0<T<1$ 时,函数 $f(x)$ 必然为 $\Omega$ 函数.
事实上,一方面 $[T]=0$,于是 $f([T])=f(0)$;另一方面函数 $f(x)$ 以 $T$ 为周期,于是 $f(T)=f(0)$.因此$$f([T])=f(T),$$函数 $f(x)$ 为 $\Omega$ 函数. -
若函数 $f(x)=x+\dfrac ax$ 是 $\Omega$ 函数,求 $a$ 的取值范围.标注答案$\left\{a\left|a\neq n^2\land a\neq n(n+1),a\in\mathbb R^+,n\in\mathbb N^{\ast}\right.\right\}$解析从单调性入手分析.
情形一 当 $a\leqslant 0$ 时,函数 $f(x)$ 在 $(-\infty,0)$ 与 $(0,+\infty)$ 上分别单调递增.因为 $x$ 与 $[x]$ 必在同一个单调区间上,所以对任意的 $x\in\mathbb R\land x\notin \mathbb Z\land x\notin (0,1)$,都有 $x>[x]$,因此$$f(x)>f([x]),$$函数 $f(x)$ 不是 $\Omega$ 函数.情形二 当 $a>0$ 时,若 $\sqrt a$ 为正整数,那么由于在每个取样区间 $[n,n+1)$($n\in\mathbb Z$)上,函数 $f(x)$ 均为单调函数,因此函数 $f(x)$ 不是 $\Omega$ 函数.当 $\sqrt a$ 不为正整数时,设 $k^2<a<(k+1)^2$($k\in\mathbb N^{\ast}$).因此只需要也必须在取样区间 $[-k-1,-k)$ 或 $[k,k+1)$ 内完成“调头”(如图6就是在 $[-k-1,-k)$ 上完成“掉头”的例子),也即$$f(-k)<f(-k-1)\lor f\left(k+1\right)>f\left(k\right) ,$$即$$-k+\dfrac{a}{-k}<-k-1+\dfrac{a}{-k-1}\lor k+1+\dfrac{a}{k+1}>k+\dfrac{a}{k},$$也即$$k+\dfrac{a}{k}\neq k+1+\dfrac{a}{k+1},$$整理得$$a\neq k(k+1),$$因此函数 $f(x)$ 当 $a\neq k(k+1)$($k\in\mathbb N^{\ast}$)时是 $\Omega$ 函数.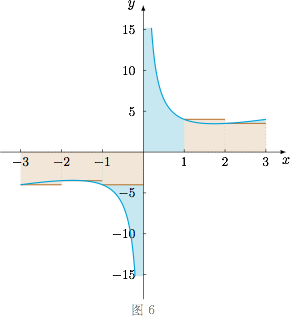 综上,$a$ 的取值范围是 $\left\{a\left|a\neq n^2\land a\neq n(n+1),a\in\mathbb R^+,n\in\mathbb N^{\ast}\right.\right\}$.
综上,$a$ 的取值范围是 $\left\{a\left|a\neq n^2\land a\neq n(n+1),a\in\mathbb R^+,n\in\mathbb N^{\ast}\right.\right\}$.情形二的另法 当 $a>0$ 时,考虑 $x\in\mathbb R\land x\notin \mathbb Z\land x\notin (0,1)$ 的条件下$$f(x)=f([x]),$$即$$x+\dfrac ax=[x]+\dfrac a{[x]},$$也即$$x-[x]-\dfrac{a\left(x-[x]\right)}{x\cdot [x]}=0,$$两边约去正数 $x-[x]$,得$$a=x\cdot [x].$$接下来只需要求出 $h(x)=x\cdot [x]$,其中 $x\in\mathbb R\land x\notin \mathbb Z$ 的值域,即为 $a$ 的取值范围.
将 $h(x)$ 的定义域划分成无数形如 $(n,n+1)$($n\in \mathbb Z$)的区间的并,因此只需要求出每一个区间 $P_n=(n,n+1)$($n\in\mathbb Z^{\ast}$,其中 $\mathbb{Z}^{\ast}$ 表示非零整数)对应的函数值取值范围 $Q_n$,再求它们的并集就可以得到函数 $h(x)$ 的值域,如图7.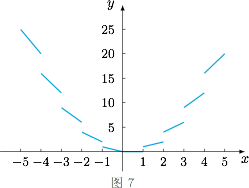 当 $x\in P_n$ 时,我们有 $[x]=n$,于是$$h(x)=x\cdot [x]=nx,$$因此$$Q_n=\begin{cases} \left(n(n+1),n^2\right),&n<0,\\ \left( n^2,n(n+1)\right),&n>0,\end{cases}$$于是它们的并,也即 $a$ 的取值范围是$$\bigcup_{n\in\mathbb Z^{\ast}}{Q_n}=\left\{a\left|a\neq n^2\land a\neq n(n+1),a\in\mathbb R^+,n\in\mathbb Z\right.\right\},$$即不为整数的平方以及相邻两个整数的乘积的所有正实数.
当 $x\in P_n$ 时,我们有 $[x]=n$,于是$$h(x)=x\cdot [x]=nx,$$因此$$Q_n=\begin{cases} \left(n(n+1),n^2\right),&n<0,\\ \left( n^2,n(n+1)\right),&n>0,\end{cases}$$于是它们的并,也即 $a$ 的取值范围是$$\bigcup_{n\in\mathbb Z^{\ast}}{Q_n}=\left\{a\left|a\neq n^2\land a\neq n(n+1),a\in\mathbb R^+,n\in\mathbb Z\right.\right\},$$即不为整数的平方以及相邻两个整数的乘积的所有正实数.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3