函数 $f(x)=(x^2-ax+2a)\ln (x+1)$ 的图象经过四个象限，求实数 $a$ 的取值范围．
【难度】
【出处】
无
【标注】
【答案】
$\left(-\dfrac 13,0\right)$
【解析】
由于当 $x>0$ 时 $\ln (x+1)>0$，当 $-1<x<0$ 时，$\ln (x+1)<0$，如图．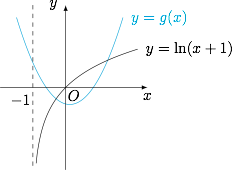
因此问题等价于函数 $g(x)=x^2-ax+2a$ 在区间 $(-1,0)$ 和区间 $(0,+\infty)$ 上各有一个零点，即$$\begin{cases} g(-1)>0,\\ g(0)<0,\end{cases}$$解得实数 $a$ 的取值范围是 $\left(-\dfrac 13,0\right)$．
因此问题等价于函数 $g(x)=x^2-ax+2a$ 在区间 $(-1,0)$ 和区间 $(0,+\infty)$ 上各有一个零点，即$$\begin{cases} g(-1)>0,\\ g(0)<0,\end{cases}$$解得实数 $a$ 的取值范围是 $\left(-\dfrac 13,0\right)$．
答案
解析
备注
