如图,正方体 $ABCD-A_1B_1C_1D_1$ 在平面 $\alpha$ 的上方,点 $O$ 是线段 $A_1C_1$ 的中点,直线 $OA$ 与平面 $\alpha$ 所成角为 $\dfrac{\pi}3$.当正方体 $ABCD-A_1B_1C_1D_1$ 绕 $OA$ 旋转一周时,求平面 $C_1D_1DC$ 与平面 $\alpha$ 所成角的正弦值的取值范围.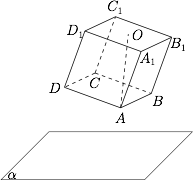

【难度】
【出处】
无
【标注】
【答案】
$\left[\dfrac{3\sqrt{10}-\sqrt 6}{12},\dfrac{3\sqrt{10}+\sqrt 6}{12}\right]$
【解析】
考虑平面 $C_1D_1DC$ 的法线 $DA$,直线 $AO$ 和平面 $\alpha$ 的法线 $AP$ 形成的三面角.
由于$$\cos\angle DAO=\dfrac{1}{\sqrt 6} , \cos\angle PAO=\dfrac {\sqrt 3}2,$$根据三射线定理,有\[\cos \langle AD,AP\rangle =\cos\angle DAO\cdot \cos\angle PAO+\sin\angle DAO\cdot \sin \angle PAO\cdot \cos\varphi,\]其中 $\varphi$ 是二面角 $D-OA-P$ 的大小.因此\[\cos \langle AD,AP\rangle =\dfrac{1}{\sqrt 6}\cdot \dfrac{\sqrt 3}2+\dfrac{\sqrt 5}{\sqrt 6}\cdot \dfrac 12\cdot \cos\varphi=\dfrac{\sqrt 3+\sqrt 5\cos\varphi}{2\sqrt 6},\]因此平面 $C_1D_1DC$ 与平面 $\alpha$ 所成角的余弦值的取值范围是$$\left[\dfrac{\sqrt 3-\sqrt 5}{2\sqrt 6},\dfrac{\sqrt 3+\sqrt 5}{2\sqrt 6}\right],$$正弦值的取值范围是$$\left[\dfrac{\sqrt{15}-1}{2\sqrt 6},\dfrac{\sqrt {15}+1}{2\sqrt 6}\right],$$即$$\left[\dfrac{3\sqrt{10}-\sqrt 6}{12},\dfrac{3\sqrt{10}+\sqrt 6}{12}\right].$$
由于$$\cos\angle DAO=\dfrac{1}{\sqrt 6} , \cos\angle PAO=\dfrac {\sqrt 3}2,$$根据三射线定理,有\[\cos \langle AD,AP\rangle =\cos\angle DAO\cdot \cos\angle PAO+\sin\angle DAO\cdot \sin \angle PAO\cdot \cos\varphi,\]其中 $\varphi$ 是二面角 $D-OA-P$ 的大小.因此\[\cos \langle AD,AP\rangle =\dfrac{1}{\sqrt 6}\cdot \dfrac{\sqrt 3}2+\dfrac{\sqrt 5}{\sqrt 6}\cdot \dfrac 12\cdot \cos\varphi=\dfrac{\sqrt 3+\sqrt 5\cos\varphi}{2\sqrt 6},\]因此平面 $C_1D_1DC$ 与平面 $\alpha$ 所成角的余弦值的取值范围是$$\left[\dfrac{\sqrt 3-\sqrt 5}{2\sqrt 6},\dfrac{\sqrt 3+\sqrt 5}{2\sqrt 6}\right],$$正弦值的取值范围是$$\left[\dfrac{\sqrt{15}-1}{2\sqrt 6},\dfrac{\sqrt {15}+1}{2\sqrt 6}\right],$$即$$\left[\dfrac{3\sqrt{10}-\sqrt 6}{12},\dfrac{3\sqrt{10}+\sqrt 6}{12}\right].$$
答案
解析
备注