查看数据源：5927916774a309000798cddc
已知动圆 $C$ 经过点 $F\left(0,1\right)$，并且与直线 $y = - 1$ 相切，若直线 $3x - 4y + 20 = 0$ 与圆 $C$ 有公共点，则圆 $C$ 的面积  \((\qquad)\)
A: 有最大值为 $ {\mathrm \pi} $
B: 有最小值为 ${\mathrm \pi} $
C: 有最大值为 $4 {\mathrm \pi} $
D: 有最小值为 $4 {\mathrm \pi} $
【难度】
【出处】
无
【标注】
  • 知识点
    >
    解析几何
    >
    抛物线
    >
    抛物线的定义
  • 知识点
    >
    解析几何
    >
    直线与圆
    >
    直线与圆的位置关系
【答案】
D
【解析】
动圆 $C$ 的圆心 $M$ 到点 $F(0,1)$ 与到直线 $y=-1$ 的距离相等，因此圆心在抛物线 $x^2=4y$ 上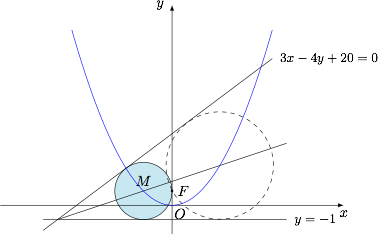．为了使得直线 $l:3x-4y+20=0$ 与圆 $C$ 有公共点，于是 $M$ 必须在直线 $l$ 与直线 $y=-1$ 所成锐角的平分线上方（包括在角平分线上）．因此圆 $C$ 的面积有最小值无最大值，排除A，C．
容易求出角平分线的方程为 $y=\dfrac 13(x+8)-1$，与抛物线 $y=\dfrac 14x^2$ 的交点坐标分别为 $(-2,1)$ 和 $\left(\dfrac {10}{3},\dfrac {25}{9}\right)$，因此圆 $C$ 的最小面积为 $4\pi$．
题目 答案 解析 备注
0.274566s