查看数据源：5927927974a309000ad0ce99
点 $ P $ 在直线 $ l:y=x-1 $ 上，若存在过 $ P $ 的直线交抛物线 $ y=x^2 $ 于 $ A,B $ 两点，且 $ |PA|=|AB| $，则称点 $ P $ 为“$\mathbb{A}$ 点”，那么下列结论中正确的是  \((\qquad)\)
A: 直线上的所有点都是“$\mathbb{A}$ 点”
B: 直线上仅有有限个点是“$\mathbb{A}$ 点”
C: 直线上的所有点都不是“$\mathbb{A}$ 点”
D: 直线上有无穷多个点（点不是所有的点）是“$\mathbb{A}$ 点”
【难度】
【出处】
无
【标注】
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的图象变换
  • 知识点
    >
    函数
    >
    常见初等函数
    >
    二次函数
【答案】
A
【解析】
记抛物线为 $C:y=x^2$，先考虑点集 $I=\{M\mid A ,B\in C ,|MA|=|AB|\}$，再考虑点集 $U=\{P\mid P\in l\}$ 与 $I$ 的关系即可．
对于点集 $I$，选定抛物线 $C$ 上任意一点 $A$，满足条件的 $M$ 的集合即为抛物线 $C$ 关于点 $A$ 对称的抛物线 $C'$．因此随着点 $A$ 在抛物线 $C$ 上移动，点集 $I$ 即为抛物线 $C$ 的外部（抛物线 $C$ 将坐标平面分为两个部分，包含焦点的部分称为内部，另外一个部分称为外部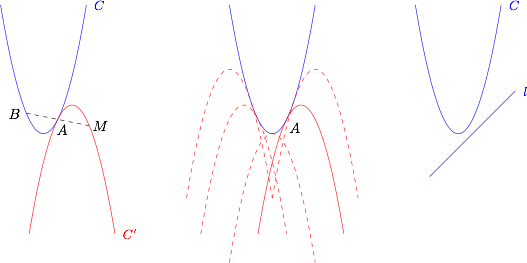）．对于 $U$，容易知道 $y=x-1$ 与 $y=x^2$ 相离，于是 $U \subseteq I$，即直线 $l$ 上的所有点都是“$\mathbb{A}$ 点”，选A．
题目 答案 解析 备注
0.122117s