如图,直角梯形 $ABCD$ 中,$AD \perp CD$,以 $A$ 为圆心 $AD$ 为半径的圆与以 $B$ 为圆心 $BC$ 为半径的圆交于 $E$、$F$ 两点,$\odot O$ 与 $\odot A$ 和 $\odot B$ 均内切,切点分别为 $G$,$H$.求证:$GD$、$EF$、$HC$ 三线共点.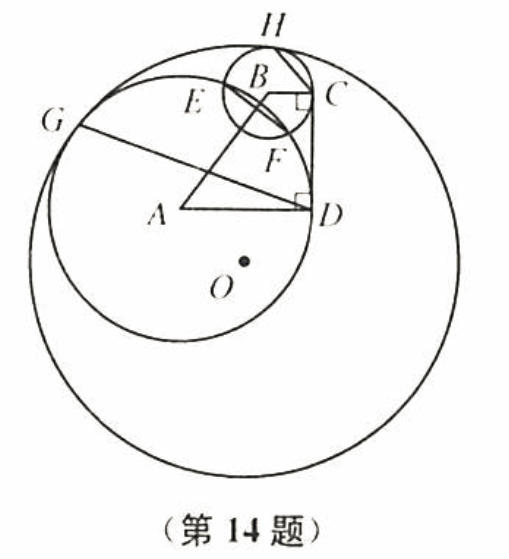

【难度】
【出处】
2017年全国高中数学联赛河北省预赛
【标注】
【答案】
略
【解析】
略
答案
解析
备注