如图,$\odot O_1$、$\odot O_2$ 相交于 $A$、$B$ 两点,$CD$ 是经过点 $A$ 的一条线段,其中点 $C$、$D$ 分别在 $\odot O_1$、$\odot O_2$ 上,过线段 $CD$ 上异于端点的任意一点 $K$,作 $KM \parallel BD$,$KN \parallel BC$,点 $M$、$N$ 分别在 $BC$、$BD$ 上,又向 $\triangle BCD$ 形外方向,作 $ME \perp BC$,$NF \perp BD$,其中 $E$ 在 $\odot O_1$ 上,$F$ 在 $\odot O_2$ 上.
证明:$KE \perp KF$.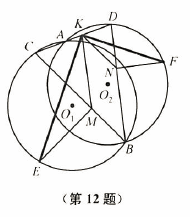
证明:$KE \perp KF$.

【难度】
【出处】
2017年全国高中数学联赛江西省预赛
【标注】
【答案】
略
【解析】
略
答案
解析
备注