设 $\triangle ABC$ 的垂心为 $H$,中点三角形的内切圆为 $\Gamma$.直线 $l\parallel AB$,$m\parallel AC$,且都与 $\Gamma$ 相切($AB,l$ 和 $AC,m$ 分别在 $S$ 同侧),$l$ 与 $m$ 交于 $T$.射线 $AT$ 上一点 $N$ 满足 $AN=2AT$,$Q$ 是优弧 $BAC$ 的中点,点 $R$ 让四边形 $AHRQ$ 成为平行四边形.证明:$HR\perp RN$.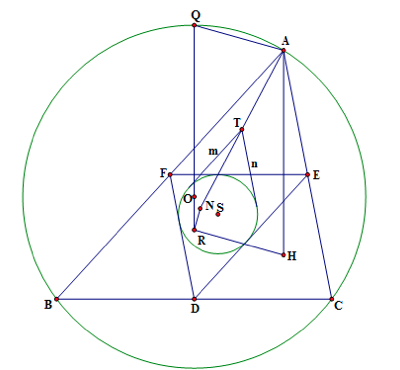

【难度】
【出处】
2015年北京大学数学秋令营试题
【标注】
【答案】
略
【解析】
略
答案
解析
备注