如图,点 $A$ 与点 $A'$ 在 $x$ 轴上,且关于 $y$ 轴对称,过点 $A'$ 垂直于 $x$ 轴的直线与抛物线 $y^2=2x$ 交于两点 $B$、$C$,点 $D$ 为线段 $AB$ 上的动点,点 $E$ 在线段 $AC$ 上,满足 $\dfrac {|CE|}{|CA|}=\dfrac {|AD|}{|AB|}$.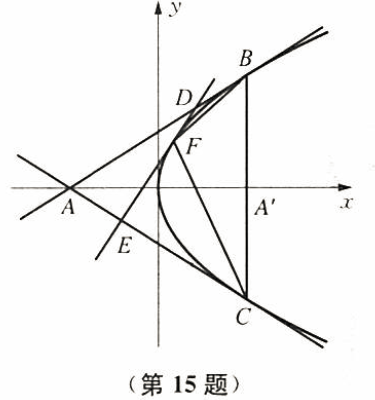

【难度】
【出处】
2017年全国高中数学联赛四川省预赛
【标注】
-
求证:直线 $DE$ 与此抛物线有且只有一个公共点;标注答案略解析略
-
设直线 $DE$ 与此抛物线的公共点为 $F$,记 $\triangle BCF$ 与 $\triangle ADE$ 的面积分别为 $S_1$、$S_2$.求 $\dfrac {S_1}{S_2}$ 的值.标注答案略解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2