已知四棱锥 $P-ABCD$ 中，$PA\perp ABCD$，$AB\perp AD$，$AD\perp CD$，$PA=AD=DC=2AB$，$M$ 为 $PC$ 中点．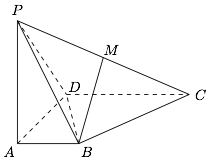
【难度】
【出处】
2014年南开大学自主招生试题（回忆版）
【标注】
-
求证：$BM\parallel$ 平面 $PAD$；标注答案略解析设 $E$ 为 $PD$ 的中点，连接 $ME,AE$，则 $ME$ 与 $AB$ 平行且相等，因此 $BM\parallel AE$，从而 $BM\parallel$ 平面 $PAD$．
-
在面 $PAD$ 内找一点 $N$，使 $MN\perp $ 面 $PBD$；标注答案$N$ 为 $\triangle PAD$ 斜边中线的中点解析以 $A$ 为坐标原点，$AB,AD,AP$ 所在直线为 $x,y,z$ 轴建立空间直角坐标系，如图，
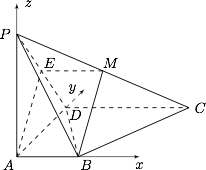则有 $A(0,0,0),B(1,0,0),C(2,2,0),P(0,0,2),M(1,1,1)$，设 $N(0,y,z)$，则有$$\overrightarrow{MN}=(-1,y-1,z-1),\overrightarrow{BP}=(-1,0,2),\overrightarrow{BD}=(-1,2,0),$$于是有$$\begin{cases}\overrightarrow{MN}\cdot\overrightarrow{BP}=1+2(z-1)=0,\\\overrightarrow{MN}\cdot\overrightarrow{BD}=1+2(y-1)=0,\end{cases}$$解得$$y=\dfrac 12,z=\dfrac 12,$$从而得到点 $N$ 的坐标为 $\left(0,\dfrac 12,\dfrac 12\right)$，即 $N$ 为 $AE$ 的中点． -
求 $PC$ 与面 $BPD$ 所成角的正弦值．标注答案$\dfrac{\sqrt 2}3$解析由（2）知 $\overrightarrow{MN}$ 为平面 $BPD$ 的一个法向量，设 $PC$ 与面 $BPD$ 所成的角为 $ \theta $，又 $\overrightarrow{MN}=\left(-1,-\dfrac 12,-\dfrac 12\right)$，$\overrightarrow{PC}=(2,2,-2)$，从而有$$\sin\theta=\left|\cos\langle\overrightarrow{MN},\overrightarrow{PC}\rangle\right|=\dfrac{\left|-2-1+1\right|}{\sqrt{1+\dfrac 14+\dfrac 14}\cdot 2\sqrt 3}=\dfrac{\sqrt 2}3.$$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
