已知四棱锥 $P-ABCD$ 中，$PA\perp ABCD$，$AB\perp AD$，$AD\perp CD$，$PA=AD=DC=2AB$，$M$ 为 $PC$ 中点．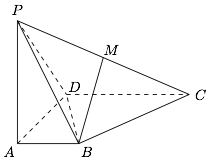
【难度】
【出处】
2014年南开大学自主招生试题（回忆版）
【标注】
-
求证：$BM\parallel$ 平面 $PAD$；标注答案略解析设 $E$ 为 $PD$ 的中点，连接 $ME$，则 $ME$ 与 $AB$ 平行且相等，因此 $BM\parallel AE$，从而 $BM\parallel$ 平面 $PAD$．
-
在面 $PAD$ 内找一点 $N$，使 $MN\perp $ 面 $PBD$；标注答案$N$ 为 $\triangle PAD$ 斜边中线的中点解析如图，连接 $AE$．由于 $AE,EM$ 均与 $PD$ 垂直，因此 $N$ 必然在直线 $AE$ 上．
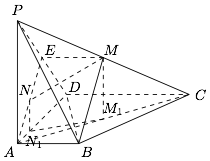作 $M$ 在底面上的投影 $M_1$，则 $M_1$ 为 $AC$ 中点，在底面 $ABCD$ 内过 $M_1$ 作 $BD$ 的垂线，交 $AD$ 于 $N_1$，则 $N_1$ 为 $AD$ 的四等分点，且 $DN_1=3N_1A$．在面 $PAD$ 内过 $N_1$ 作 $AD$ 的垂线 $l$，则由于 $M_1N_1\perp BD$，于是 $N$ 必然在直线 $l$ 上．因此 $N$ 为直线 $l$ 与 $AE$ 的交点，也即 $AE$ 的中点． -
求 $PC$ 与面 $BPD$ 所成角的正弦值．标注答案$\dfrac{\sqrt 2}3$解析设 $PC$ 与面 $BPD$ 所成的角为 $ \theta $，记 $ \angle BPC=\alpha $，$ \angle CPD=\beta $，$ \angle BPD=\gamma$，则\[\begin{split} \cos\theta&=\dfrac{\sqrt{\cos^2\alpha+\cos^2\beta-2\cos\alpha\cos\beta\cos\gamma}}{\sin\gamma}\\
&=\dfrac{\sqrt{\dfrac 35+\dfrac 23-2\cdot\dfrac{\sqrt 3}{\sqrt 5}\cdot \dfrac{\sqrt 2}{\sqrt 3}\cdot \dfrac{\sqrt 2}{\sqrt 5}}}{\dfrac{\sqrt 3}{\sqrt 5}}\\
&=\dfrac{\sqrt 7}3,\end{split}\]于是所求正弦值为 $\dfrac{\sqrt 2}3$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3
