如图,$\odot O_1$ 与 $\odot O_2$ 相交于 $A$、$B$ 两点,直线 $PQ$ 是两圆距离点 $B$ 较近的共切线,且分别与 $\odot O_1$、$\odot O_2$ 切于点 $P$、$Q$.设 $QB$、$PB$ 的延长线分别交 $AP$、$AQ$ 于点 $C$、$D$.求证:$AC \cdot BC=AD \cdot BD$.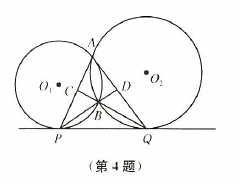

【难度】
【出处】
2017年全国高中数学联赛陕西省预赛(二试)
【标注】
【答案】
略
【解析】
略
答案
解析
备注