如图,在四边形 $ABCD$ 中,$BC=2$,$\angle B=45^\circ$,$AD=\sqrt 3 AC$,$\angle DAC=2\angle ACB$.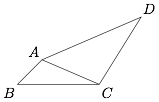

【难度】
【出处】
无
【标注】
-
求 $CD$ 的最小值;标注答案$\sqrt 2$解析如图,过 $A$ 作 $BC$ 的平行线,截取 $AE=\sqrt 3BC$,连接 $DE$.
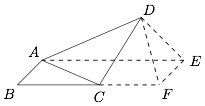 由于 $\angle DAE=\angle ACB$ 且\[\dfrac{AC}{AD}=\dfrac{BC}{AE}=\dfrac{1}{\sqrt 3},\]于是 $\triangle ACB$ 与 $\triangle DAE$ 相似.过 $E$ 作 $AB$ 的平行线,与直线 $BC$ 交于点 $F$,连接 $DF$,则\[\angle DEF=\angle DEA+\angle AEF=\angle DEA+\angle B=90^\circ,\]又\[\dfrac{AB}{DE}=\dfrac{EF}{DE}=\dfrac{1}{\sqrt 3},\]因此\[\angle DFB=\angle BFE-\angle DFE=75^\circ,\]从而点 $D$ 的轨迹是从 $F$ 出发的一条射线(不包含端点).不难求出 $CD$ 的最小值为 $C$ 到该射线 $l$ 的距离,为\[CF\cdot \sin 75^\circ=(2\sqrt 3-2)\cdot \dfrac{\sqrt 6+\sqrt 2}4=\sqrt 2.\]
由于 $\angle DAE=\angle ACB$ 且\[\dfrac{AC}{AD}=\dfrac{BC}{AE}=\dfrac{1}{\sqrt 3},\]于是 $\triangle ACB$ 与 $\triangle DAE$ 相似.过 $E$ 作 $AB$ 的平行线,与直线 $BC$ 交于点 $F$,连接 $DF$,则\[\angle DEF=\angle DEA+\angle AEF=\angle DEA+\angle B=90^\circ,\]又\[\dfrac{AB}{DE}=\dfrac{EF}{DE}=\dfrac{1}{\sqrt 3},\]因此\[\angle DFB=\angle BFE-\angle DFE=75^\circ,\]从而点 $D$ 的轨迹是从 $F$ 出发的一条射线(不包含端点).不难求出 $CD$ 的最小值为 $C$ 到该射线 $l$ 的距离,为\[CF\cdot \sin 75^\circ=(2\sqrt 3-2)\cdot \dfrac{\sqrt 6+\sqrt 2}4=\sqrt 2.\] -
求 $\tan \angle D$ 的最大值.标注答案$\dfrac{\sqrt 2}{2}$解析设 $\angle ACB=\theta$,则 $\angle DAC=2\theta$,于是在 $\triangle DAC$ 中应用余弦定理,有\[CD^2=AD^2+AC^2-2\cdot AD\cdot AC\cdot \cos2\theta,\]可得\[CD^2=\left(4-2\sqrt 3\right)\cos2\theta\cdot AC^2,\]再利用正弦定理,有\[\dfrac{CD}{\sin 2\theta}=\dfrac{AC}{\sin\angle D},\]于是\[\begin{split} \sin\angle D&=\dfrac{AC}{CD}\cdot \sin2\theta\\
&=\dfrac{\sin 2\theta}{\sqrt{4-2\sqrt 3\cos 2\theta}}\\
&=\sqrt{\dfrac{1-\cos^22\theta}{4-2\sqrt 3\cos2\theta}}\\
&=\sqrt{\dfrac 23-\left[\dfrac{\sqrt 3}6\left(\dfrac{2}{\sqrt 3}-\cos2\theta\right)+\dfrac{1}{6\sqrt 3}\cdot \dfrac{1}{\dfrac{2}{\sqrt 3}-\cos2\theta}\right]}\\
&\leqslant\dfrac{\sqrt{3}}3,\end{split}\]等号当 $\cos 2\theta=\dfrac{\sqrt 3}3$ 时取得.进而可得 $\tan \angle D$ 的最大值为 $\dfrac{\sqrt 2}{2}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2