如图所示,已知圆内接四边形 $ABCD$ 中,$AC$ 和 $BD$ 相交于 $P$ 点,满足 $\dfrac {AB}{AD}=\dfrac {CB}{CD}$.设 $E$ 为 $AC$ 的中点,求证:$\dfrac {BE}{ED}=\dfrac {BP}{PD}$.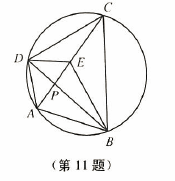

【难度】
【出处】
2017年全国高中数学联赛广西壮族自治区预赛
【标注】
【答案】
略
【解析】
略
答案
解析
备注